Математические модели

Математическая модель - приближенное описание объекта моделирования, выраженное с помощью математической символики.

Математические модели появились вместе с математикой много веков назад. Огромный толчок развитию математического моделирования придало появление ЭВМ. Применение вычислительных машин позволило проанализировать и применить на практике многие математические модели, которые раньше не поддавались аналитическому исследованию. Реализованная на компьютере математическая модель называетсякомпьютерной математической моделью, а проведение целенаправленных расчетов с помощью компьютерной модели называется вычислительным экспериментом.

Этапы компьютерного математического моделирования изображены на рисунке. Первый этап -определение целей моделирования. Эти цели могут быть различными:

1. модель нужна для того, чтобы понять, как устроен конкретный объект, какова его структура, основные свойства, законы развития и взаимодействия
с окружающим миром (понимание);

2. модель нужна для того, чтобы научиться управлять объектом (или процессом) и определить наилучшие способы управления при заданных целях и критериях (управление);

3. модель нужна для того, чтобы прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект (прогнозирование).

Поясним на примерах. Пусть объект исследования - взаимодействие потока жидкости или газа с телом, являющимся для этого потока препятствием. Опыт показывает, что сила сопротивления потоку со стороны тела растет с ростом скорости потока, но при некоторой достаточно высокой скорости эта сила скачком уменьшается с тем, чтобы с дальнейшим увеличением скорости снова возрасти. Что же вызвало уменьшение силы сопротивления? Математическое моделирование позволяет получить четкий ответ: в момент скачкообразного уменьшения сопротивления вихри, образующиеся в потоке жидкости или газа позади обтекаемого тела, начинают отрываться от него и уноситься потоком.

Пример совсем из другой области: мирно сосуществовавшие со стабильными численностями популяции двух видов особей, имеющих общую кормовую базу, "вдруг" начинают резко менять численность. И здесь математическое моделирование позволяет (с известной долей достоверности) установить причину (или по крайней мере опровергнуть определенную гипотезу).

Выработка концепции управления объектом - другая возможная цель моделирования. Какой режим полета самолета выбрать для того, чтобы полет был безопасным и экономически наиболее выгодным? Как составить график выполнения сотен видов работ на строительстве большого объекта, чтобы оно закончилось в максимально короткий срок? Множество таких проблем систематически возникает перед экономистами, конструкторами, учеными.

Наконец, прогнозирование последствий тех или иных воздействий на объект может быть как относительно простым делом в несложных физических системах, так и чрезвычайно сложным - на грани выполнимости - в системах биолого-экономических, социальных. Если ответить на вопрос об изменении режима распространения тепла в тонком стержне при изменениях в составляющем его сплаве относительно легко, то проследить (предсказать) экологические и климатические последствия строительства крупной ГЭС или социальные последствия изменений налогового законодательства несравненно труднее. Возможно, и здесь методы математического моделирования будут оказывать в будущем более значительную помощь.

Второй этап: определение входных и выходных параметров модели; разделение входных параметров по степени важности влияния их изменений на выходные. Такой процесс называется ранжированием, или разделением по рангам (см. "Формализация и моделирование" ).

Третий этап: построение математической модели. На этом этапе происходит переход от абстрактной формулировки модели к формулировке, имеющей конкретное математическое представление. Математическая модель - это уравнения, системы уравнений, системы неравенств, дифференциальные уравнения или системы таких уравнений и пр.

Четвертый этап: выбор метода исследования математической модели. Чаще всего здесь используются численные методы, которые хорошо поддаются программированию. Как правило, для решения одной и той же задачи подходит несколько методов, различающихся точностью, устойчивостью и т.д. От верного выбора метода часто зависит успех всего процесса моделирования.

Пятый этап: разработка алгоритма, составление и отладка программы для ЭВМ - трудно формализуемый процесс. Из языков программирования многие профессионалы для математического моделирования предпочитают FORTRAN: как в силу традиций, так и в силу непревзойденной эффективности компиляторов (для расчетных работ) и наличия написанных на нем огромных, тщательно отлаженных и оптимизированных библиотек стандартных программ математических методов. В ходу и такие языки, как PASCAL, BASIC, С, - в зависимости от характера задачи и склонностей программиста.

Шестой этап: тестирование программы. Работа программы проверяется на тестовой задаче с заранее известным ответом. Это - лишь начало процедуры тестирования, которую трудно описать формально исчерпывающим образом. Обычно тестирование заканчивается тогда, когда пользователь по своим профессиональным признакам сочтет программу верной.

Седьмой этап: собственно вычислительный эксперимент, в процессе которого выясняется, соответствует ли модель реальному объекту (процессу). Модель достаточно адекватна реальному процессу, если некоторые характеристики процесса, полученные на ЭВМ, совпадают с экспериментально полученными характеристиками с заданной степенью точности. В случае несоответствия модели реальному процессу возвращаемся к одному из предыдущих этапов.

Классификация математических моделей

В основу классификации математических моделей можно положить различные принципы. Можно классифицировать модели по отраслям наук (математические модели в физике, биологии, социологии и т.д.). Можно классифицировать по применяемому математическому аппарату (модели, основанные на применении обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, стохастических методов, дискретных алгебраических преобразований и т.д.). Наконец, если исходить из общих задач моделирования в разных науках безотносительно к математическому аппарату, наиболее естественна такая классификация:

• дескриптивные (описательные) модели;
• оптимизационные модели;
• многокритериальные модели;
• игровые модели.

Поясним это на примерах.

Дескриптивные (описательные) модели. Например, моделирование движения кометы, вторгшейся в Солнечную систему, производится с целью предсказания траектории ее полета, расстояния, на котором она пройдет от Земли, и т.д. В этом случае цели моделирования носят описательный характер, поскольку нет никаких возможностей повлиять на движение кометы, что-то в нем изменить.

Оптимизационные модели используются для описания процессов, на которые можно воздействовать, пытаясь добиться достижения заданной цели. В этом случае в модель входит один или несколько параметров, доступных влиянию. Например, меняя тепловой режим в зернохранилище, можно задаться целью подобрать такой режим, чтобы достичь максимальной сохранности зерна, т.е. оптимизировать процесс хранения.

Многокритериальные модели. Нередко приходится оптимизировать процесс по нескольким параметрам одновременно, причем цели могут быть весьма противоречивыми. Например, зная цены на продукты и потребность человека в пище, нужно организовать питание больших групп людей (в армии, детском летнем лагере и др.) физиологически правильно и, одновременно с этим, как можно дешевле. Ясно, что эти цели совсем не совпадают, т.е. при моделировании будет использоваться несколько критериев, между которыми нужно искать баланс.

Игровые модели могут иметь отношение не только к компьютерным играм, но и к весьма серьезным вещам. Например, полководец перед сражением при наличии неполной информации о противостоящей армии должен разработать план: в каком порядке вводить в бой те или иные части и т.д., учитывая и возможную реакцию противника. Есть специальный раздел современной математики - теория игр, - изучающий методы принятия решений в условиях неполной информации.

В школьном курсе информатики начальное представление о компьютерном математическом моделировании ученики получают в рамках базового курса. В старших классах математическое моделирование может глубоко изучаться в общеобразовательном курсе для классов физико-математического профиля, а также в рамках специализированного элективного курса.

Основными формами обучения компьютерному математическому моделированию в старших классах являются лекционные, лабораторные и зачетные занятия. Обычно работа по созданию и подготовке к изучению каждой новой модели занимает 3-4 урока. В ходе изложения материала ставятся задачи, которые в дальнейшем должны быть решены учащимися самостоятельно, в общих чертах намечаются пути их решения. Формулируются вопросы, ответы на которые должны быть получены при выполнении заданий. Указывается дополнительная литература, позволяющая получить вспомогательные сведения для более успешного выполнения заданий.

Формой организации занятий при изучении нового материала обычно служит лекция. После завершения обсуждения очередной модели учащиеся имеют в своем распоряжении необходимые теоретические сведения и набор заданий для дальнейшей работы. В ходе подготовки к выполнению задания учащиеся выбирают подходящий метод решения, с помощью какого-либо известного частного решения тестируют разработанную программу. В случае вполне возможных затруднений при выполнении заданий дается консультация, делается предложение более детально проработать указанные разделы в литературных источниках.

Наиболее соответствующим практической части обучения компьютерному моделированию является метод проектов. Задание формулируется для ученика в виде учебного проекта и выполняется в течение нескольких уроков, причем основной организационной формой при этом являются компьютерные лабораторные работы. Обучение моделированию с помощью метода учебных проектов может быть реализовано на разных уровнях. Первый - проблемное изложение процесса выполнения проекта, которое ведет учитель. Второй - выполнение проекта учащимися под руководством учителя. Третий - самостоятельное выполнение учащимися учебного исследовательского проекта.

Результаты работы должны быть представлены в численном виде, в виде графиков, диаграмм. Если имеется возможность, процесс представляется на экране ЭВМ в динамике. По окончанию расчетов и получению результатов проводится их анализ, сравнение с известными фактами из теории, подтверждается достоверность и проводится содержательная интерпретация, что в дальнейшем отражается в письменном отчете.

Если результаты удовлетворяют ученика и учителя, то работа считается завершенной, и ее конечным этапом является составление отчета. Отчет включает в себя краткие теоретические сведения по изучаемой теме, математическую постановку задачи, алгоритм решения и его обоснование, программу для ЭВМ, результаты работы программы, анализ результатов и выводы, список использованной литературы.

Когда все отчеты составлены, на зачетном занятии учащиеся выступают с краткими сообщениями о проделанной работе, защищают свой проект. Это является эффективной формой отчета группы, выполняющей проект, перед классом, включая постановку задачи, построение формальной модели, выбор методов работы с моделью, реализацию модели на компьютере, работу с готовой моделью, интерпретацию полученных результатов, прогнозирование. В итоге учащиеся могут получить две оценки: первую - за проработанность проекта и успешность его защиты, вторую - за программу, оптимальность ее алгоритма, интерфейс и т.д. Учащиеся получают отметки и в ходе опросов по теории.

Существенный вопрос - каким инструментарием пользоваться в школьном курсе информатики для математического моделирования? Компьютерная реализация моделей может быть осуществлена:

• с помощью табличного процессора (как правило, MS Excel);
• путем создания программ на традиционных языках программирования (Паскаль, Бейсик и др.), а также на их современных версиях (Delphi, Visual
  Basic for Application и т.п.);
• с помощью специальных пакетов прикладных программ для решения математических задач (MathCAD и т.п.).

На уровне основной школы первое средство представляется более предпочтительным. Однако в старшей школе, когда программирование является, наряду с моделированием, ключевой темой информатики, желательно привлекать его в качестве инструмента моделирования. В процессе программирования учащимся становятся доступными детали математических процедур; более того, они просто вынуждены их осваивать, а это способствует и математическому образованию. Что же касается использования специальных пакетов программ, то это уместно в профильном курсе информатики в качестве дополнения к другим инструментам.

Сформулируем основные требования, предъявляемые к модели М процесса функционирования системы (объекта):

1) полнота модели должна предоставлять пользователю возможность получения необходимого набора оценок характеристик системы с требуемой точностью и достоверностью.

2) гибкость модели должна давать возможность воспроизведения различных ситуаций при варьировании структуры, параметров системы.

3) длительность разработки модели должна быть по возможности минимальной.

4) структура модели должна быть блочной, т.е. допускать возможность замены, добавления и исключения некоторых частей без переделки всей модели.

5) программные и технические средства должны обеспечивать эффективную по быстродействию и памяти программную реализацию модели.

1.3. Классификация математических моделей

В качестве основания для классификации математических моделей очень удобно выбрать такой явный признак, как тип моделируемого объекта. По типу исследуемого объекта различают математические модели технических устройств, технологических процессов, производств, предприятий.

Каждую из выделенных групп моделей в свою очередь можно разбить на ряд групп и подгрупп в зависимости от принятых для них классификационных признаков. В качестве последних наиболее часто используют факторы времени (непрерывные и дискретные модели), описываемый в модели режим работы объекта (динамический и статический), вид функциональной связи (линейная или нелинейная).

Например, на этой основе можно классифицировать математические модели технических объектов и устройств, выделив восемь групп моделей

В зависимости от характера отображаемых свойств математические модели делятся на функциональные и структурные. Функциональные модели отображают процессы, протекающие в объекте. Чаще всего эти модели задаются в виде систем уравнений.

Структурные модели применяются в задачах проектирования, связанных с описанием облика изделия, в задачах конструкторского проектирования. Это модели, отображающие геометрические свойства объекта (элементы, из которых состоит объект и характер связей между элементами). Эти математические модели имеют форму матриц, графов и т.п.

По способу построения математических моделей выделяются класс формальных (экспериментально-статистических) математических моделей и класс неформальных (аналитических) моделей.

Формальные математические модели создаются по результатам экспериментальных наблюдений за некоторым объектом-аналогом. Уравнения связи Y=F(X, Z) носят условный характер и не отражают внутренней структуры, конструктивных и технологических особенностей объекта.

Математические модели технических объектов и устройств

Непрерывные
		Дискретные
во времени		во времени
		Y=f(k, t), k=1,2,
Стохастические		Детерминированные

Рис.1.4. Классификация математических моделей

Неформальные модели создаются на основе универсальных уравнений сохранения (массы, энергии, импульса). Уравнения связи Y=F(X, Z) отражают общие законы сохранения, элементарные физико-химические процессы, протекающие в объекте.

По виду функциональной связи между входными и выходными параметрами (F(X, Z)) принято выделять линейные и нелинейные математические модели.

Задачи исследования объекта могут ограничиваться определенным режимом его функционирования. В соответствии с этим признаком выделяются модели статики и динамики.

Математическая модель динамики описывает переходный режим работы объекта и отображает изменение во времени выходных координат (Y(t)) объекта.

При разработке математической модели динамики детерминированного объекта используют различные виды дифференциальных уравнений.

1. Для описания модели динамики стационарного объекта с сосредоточенными координатами применяют обыкновенные дифференциальные уравнения или передаточные функции:

2. Для описания модели динамики стационарного объекта с распреде дифференциальные уравнения в частных производных:

	∂Y		∂Y	Y(t,z),X(t,z),B) = 0 .
	∂t		∂z

3. Для описания модели динамики нестационарного объекта с сосредоточенными координатами применяют обыкновенные дифференциальные уравнения или передаточные функции с переменными во времени коэффициентами:

		Y(t), X(t),B(t)) = 0	или, например, W =
						T(t)p + 1

4. Для описания модели динамики нестационарного объекта с распределенными координатами применяют дифференциальные уравнения в частных производных с переменными во времени коэффициентами:

	∂Y		∂Y	Y(t,z),X(t,z),B(t)) = 0 .
	∂t		∂z

Математическая модель статики описывает установившийся режим работы объекта (dY dt = 0 ) и отображает зависимость выходных координат объ-

екта (Y) от его входных координат (X).

При разработке математической модели статики детерминированного объекта используют различные виды конечных и дифференциальных уравнений.

5. Для описания модели статики стационарного объекта с сосредоточенными координатами применяют алгебраические (конечные) уравнения

f (Y , X , B ) = 0 .

		f (Y , X , B) = 0.
	Для описания модели статики			стационарного объекта	с распреде-
ленными координатами применяют				обыкновенные дифференциальные
уравнения:
			Y (z ), X (z ), B ) = 0 .
	Для описания модели статики			нестационарного объекта	с сосредо-

точенными координатами применяют конечные уравнения с переменными во времени коэффициентами:

f (Y , X , B (t )) = 0 .
8. Для описания модели статики	нестационарного объекта	с распреде-
ленными координатами применяют	дифференциальные уравнения с пере-
менными во времени коэффициентами:
f (∂ Y ,Y (z ), X (z ), B (t )) = 0 .
∂z

1.4. Понятие об адекватности математической модели

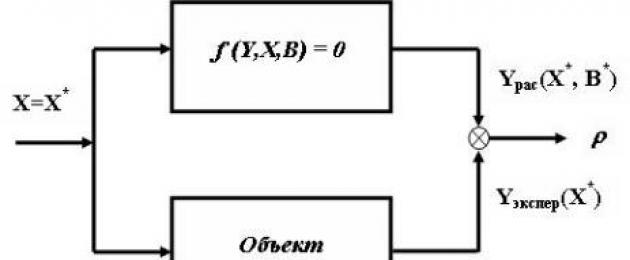
Пусть математическая модель задана в виде уравнения статики: (1.12)

Имеется объект (оригинал), на вход которого можно подать некоторое возмущение, установив новое значение вектора входных координат X = X * . Используя эти значения в уравнении (1.12), можно найти расчет-

ные значения вектора выходных координат Y рас (X * , B * ) . Сравнивая этот

вектор с соответствующими значениями, полученными в ходе эксперимента на объекте (оригинале), можно сделать вывод о степени близости модели к оригиналу (рис.1.5).

между Y рас (X * , B * ) и вектором Y эсп (X * ) , полученном на объекте при X = X * , меньше заданного числа, т.е.

ρ [ Y (X * , B* ), Y (X * ) ] < .

где ρ – функция невязки, определяет формулу для расчета расстояния;

– допустимая ошибка, характеризует степень адекватности модели.

Рис.1.5. Определение адекватности модели объекта

Адекватность модели зависит от степени полноты и достоверности сведений об исследуемом объекте, степени детализации модели, точности идентификации параметров модели, уровня подготовки и опыта исследователя.

1.5. Общая характеристика методов составления математических моделей

Анализ любого метода разработки математической модели позволяет выделить три необходимых этапа в решении этой задачи:

определение структуры функции связи f входных X и выходных Y координат объекта (формирование в общем виде уравнения математической модели);

определение параметров модели (коэффициентов уравнения математической модели) B. Задача идентификации вектора параметров В;

проверка адекватности математической модели.

В зависимости от способов решения задач первого и второго этапов различают три группы методов составления математических моделей: формальные (экспериментально-статистические методы), неформальные (аналитические методы) и комбинированные методы.

Формальные (экспериментально-статистические) методы применяются для построения математических моделей стационарных и нестационарных объектов, только с сосредоточенными координатами. Главными особенностями этих методов являются:

одинаковые с точностью до В формальные математические модели

могут описывать разные БТС; не требуется глубокое изучение особенностей моделируемого объекта;

точность математической модели достигается путем повышения размерности вектора параметров (коэффициентов) В.

В основе формальных методов построения математических моделей лежит кибернетическое представление об объекте моделирования, как о некотором черном ящике (рис.1.6).

Рис.1.6. Блок - схема объекта моделирования

В рамках данного понятия предполагается, что:

- внутренняя структура объекта неизвестна,

- доступны для наблюдения все входы (X) и выходы (Y) объекта,

- на вход объекта можно подавать различные возмущения,

- на основе наблюдений за X и Y можно составить уравнения связи, которые в дальнейшем будут рассматриваться как уравнения математической модели объекта.

Одним из главных достоинств этой группы методов является их универсальность и полная инвариантность к исследуемой предметной области. Их использование предполагает наличие у разработчика значительного объема экспериментальных данных: результатов наблюдений (Х и Y) за объектом. Очевидно, экспериментально-статистические методы нельзя применять для построения новых объектов, объектов, находящихся в стадии проектирования, не существующих в реальности.

Особенности неформальных (аналитических) методов составления математических моделей включают факты:

Функцию связи f входных X и выходных Y координат выводят на основе анализа элементарных физико-химических процессов, протекающих в объекте моделирования;

В составляющие вектора В параметров модели (коэффициенты уравнений) входят основные конструктивные и технологические характеристики моделируемого объекта;

Полученные на основе этих методов математические модели, как правило, являются нелинейными.

Основным достоинством аналитических методов построения моделей

является возможность детального (полного) анализа характеристик объекта в широком диапазоне изменения исходных данных. Однако аналитический подход к разработке математических моделей возможен только при рассмотрении сравнительно простых объектов, в других случаях он требует значительных упрощений (допущений) описаний реальных процессов, что приводит к снижению точности моделирования. Аналитические методы разработки математических моделей не требуют постановки экспериментов и могут применяться при проведении предпроектных исследований, а также при проектировании нового объекта.

Комбинированные методы представляют собой интеграцию аналитического и формально-статистического подходов к разработке математических моделей. Например, формирование в общем виде уравнений математической модели осуществляется на основе универсальных законов сохранения (аналитический подход), а определение параметров модели выполняется экспериментально-статистическими методами. При таком подходе ослабляется главный недостаток формальных методов построения моделей: отсутствие в структуре уравнений отображения элементарных физи- ко-химических процессов, протекающих в исследуемом объекте.

Контрольные вопросы

1. Какие виды моделирования вы знаете?

2. Какой принцип лежит в основе физического моделирования?

3. Какой принцип лежит в основе математического моделирования?

4. В каком виде может быть представлена физическая модель?

5. Основные достоинство и недостатки физического моделирования.

6. В каком виде может быть представлена математическая модель?

7. Достоинства и недостатки математического моделирования.

8. Характеристические признаки имитационного моделирования.

9. Какие классификационные признаки используются для выделения отдельных классов математических моделей?

10. Что описывает математическая модель динамики?

11. Какие классы математических моделей динамики вы знаете?

12. Что описывает математическая модель статики?

13. Какие классы математических моделей статики вы знаете?

14. Перечислите этапы разработки математической модели объекта.

15. Как вы понимаете утверждение "Модель адекватна объекту"?

16. Назовите группы методов составления математических моделей.

17. Какие особенности формальных методов построения математических моделей вы знаете?

18. Особенности аналитических методов построения моделей.

Математические модели, составляют абстрактную часть спектра (рис. 7.2), в целях удобства их использования в различных отраслях, в том числе и в логистике, классифицируют по шести наиболее представительными признакам:

Способа получения модели;

Способа описания или представление объекта или его свойств;

Способа формализации объекта или его свойств;

Принадлежности к иерархического уровня;

Степени масштабности описания объекта или его свойств;

Степени сложности описания объекта или его свойств.

По способу получения модели делятся на теоретические , нейронные (персептроны) и эмпирические .

Теоретические модели выводятся математически на основе знания первичных законов классической механики, электродинамики, химии и т.д. Модели, полученные из реальной жизни на основе статистической обработки результатов наблюдений, формируют группу эмпирических. Проблема построения эмпирической модели включает и выбор формы этой модели, подходящей, а также разумной степени ее сложности, совместим с имеющимися экспериментальными данными.

За последние годы в области моделирования экономических процессов все большее значение приобретают нейронные модели (персептроны). Нейронная модель (персептрон) состоит из бинарных нейроподобных элементов и имеет простую топологию.

Самый персептрон включает в себя матрицы бинарных входов (сенсорных нейронов или сетчатки, куда подаются входные образы), набора бинарных нейроподобних элементов с фиксированными связями к подмножеств сетчатки, бинарного Нейроподобная элемента с модифицированными связями в этих предикатов (элементов, решают) .

Предварительно персептрон использовался для решения задачи автоматической классификации, в общем состоит в разделении пространства признаков между заданным количеством классов. В сегодняшних условиях на уровне нейронных сетей можно решить проблему логистического прогнозирования, которая формализуется через задачу распознавания образов.

Рассмотрим следующий пример. Есть данные по текущему спросу на продукцию фирмы за шесть лет (Ас = 6): 71, 80, 101, 84, 60, 73.

Для формализации задачи используем метод окон. Зададим размеры окон η = 3, т = 1 и уровень возбуждения Нейроподобная элемента s = 1. Далее, с помощью метода окон с уже фиксированными параметрами n, т, s для нейронной сети генерируется следующая обучающая выборка:

Как видим, каждый последующий вектор образуется в результате сдвига окон W и и W 0 вправо на один элемент (s = 1). При этом предполагается наличие скрытых зависимостей во временной последовательности как множестве наблюдений.

Нейронная сеть, обучаясь на этих наблюдениях и соответственно настраивая свои коэффициенты, пытается извлечь эти закономерности и сформировать в результате ожидаемую функцию прогноза, то есть "построить" модель . Прогнозирование осуществляется по тому же принципу, что и формирование обучающей выборки.

По способу описания объекта модели делятся следующим образом:

1) алгебраические;

2) регрессионно-корреляционные;

3) вероятностно-статистические, объединяющих в себе модели теории очередей, модели запасов и статистические модели;

4) математического программирования - линейного программирования, сетевые (поточные).

Относительно первой группы моделей - алгебраических , необходимо сразу оговориться, что они по сути своей для логиста носят вспомогательный характер для принятия правильного решения. Алгебраические модели используются обычно при решении таких задач, как анализ "критической точки" и анализ "затраты - прибыль".

Регрессионно-корреляционные модели , представляющие вторую группу, является обобщением экстраполяционных и статистических моделей и используются для описания специфики объекта или его свойств.

Третью группу составляют вероятностно-статистические модели , основанные на фенологических явлениях и гипотезах. Данные модели могут быть детерминированными или стохастическими. Так, например, зависимость В = φ (Χ), которая установлена по результатам наблюдений случайных величин X и В методом наименьших квадратов, представляет собой детерминированную модель. Если же учесть наблюдаемые в результате опытов случайные отклонения экспериментальных точек от кривой У = φ (Х) и записать зависимость В от X в виде В = φ (Χ) + Ζ (где Ζ - некоторая случайная величина), то получим стохастической модели в ее идеальном выражении.

При этом величины X и В могут быть как скалярными, так и векторными. Функция φ (Χ) может быть как линейной комбинацией этих функций, так и данной нелинейной функцией, параметры которой определяются методом наименьших квадратов.

Модели линейного программирования все шире используются для решения задач логистической направленности.

Кто знаком с математическим программированием, тот знает, что ее решить в общем виде практически невозможно. Однако наиболее разработанными в математическом программировании есть задачи линейного программирования.

В задачах линейного программирования целевая функция линейная, а условия-ограничения включают линейные равенства и линейные неравенства; переменные могут быть подчинены или не подчинены требованию непреложности.

Для демонстрации простоты решений логистических задач с помощью линейного программирования обратимся к двум известным задач:

Первая - о бабку, что собирается на рынок, чтобы продать живность, которая выросла у нее во дворе за год;

Вторая - о питании.

Задача первая (о бабку)

Суть данной задачи сводится к получению ответа на простой вопрос: "Сколько надо взять бабки для продажи на рынке живых гусей, уток и кур, чтобы она получила наибольшую выручку при условии, что она может доставить на рынок живности массой не более Р кг?". При этом известны:

Масса курицы (т,), утки (т 2 ) и гуся (т3)

Стоимость курицы (с7), утки (с2) и гуся (с3).

Рассмотрим алгоритм решения задачи.

1. Для решения задачи обозначим количество, соответственно, кур - х 1 уток - х 2, гусей - х 3, взятых бабкой для продажи на рынок.

2. Составим целевую функцию этой задачи:

3. Опишем ограничения на решение задачи.

Масса товара, бабка может доставить одновременно на рынок, не должна превысить Р килограмм:

Значение , и должны быть положительными целыми числами (), то есть:

Выполнив три описанных шаги, получаем задачу линейного программирования. Подставляя исходные значения х, т, с и Р, находим ответ на поставленный вопрос.

Задача вторая (о питании)

Кафе "Бистро" ежедневно в магазине закупает продукты питания для приготовления определенных блюд для своих посетителей. В рацион входят три различных питательных вещества (b ) и нужно их, соответственно, не менее b 1, b 2, b 3 единиц. В магазине продается пять видов различных продуктов х 1 - х 5 по цене, соответственно, С-И - с 5.

Каждая единица продукта i-го вида (х i) содержит а иj единиц j-й питательного вещества, то есть, например, а 2 с показывает, что в единицы второго продукта третьей питательного вещества будет а 23 единиц.

Поскольку кафе работает в окружении конкурентов, необходимо правильно определить количество продуктов каждого вида х 1 - x 5, которые стоит закупить. При этом надо выполнить следующие условия:

1) чтобы стоимость продуктов была минимальной;

2) чтобы в рационе блюд в нужном количестве содержались все необходимые питательные вещества.

Математическая постановка решения задачи будет следующая:

1. Целевая функция данной задачи - минимизировать стоимость продуктов х 1 - х 5. Математически это будет выглядеть следующим образом:

2. Условия ограничения решения задачи:

а) количество первой питательного вещества должна быть не менее b 1 ,:

б) количество второй питательного вещества должна быть не менее b 2 :

в) количество третьей питательного вещества должна быть не менее b 3:

При этом следует иметь в виду, что количество продуктов не может иметь отрицательное число, то есть:

Для правильного понимания решения приведенной задачи рассмотрим следующий пример.

Пусть в данной задачи будем иметь следующие исходные данные:

Целевая функция будет иметь следующий вид:

Определять минимальное значение функции надо при условии выполнения следующих ограничений:

Имея в виду, что количество продуктов не может быть отрицательным числом, принимаем, что

В результате решения задачи по представленным исходным данным имеем следующий ответ: и . При данных значениях целевая функция будет иметь следующее значение:

Сетевые (поточные) модели.

Важным классом задач математического программирования являются так называемые сетевые (поточные) задачи, в терминах которых могут быть сформулированы задачи линейного программирования.

Рассмотрим в качестве примера так называемую транспортную задачу (рис. 7.3), что является одной из первых потоковых задач, которая была решена в 1941 г.. Ф.Л. Хитчкок.

Пусть есть два завода (1 и 2) и три состава (А, Б, В). Заводы производят, соответственно, s1 и s2 единиц продукции. Склады имеют возможность принять на хранение d1, d2 и d3 единиц продукции, то есть:

Задача состоит в том, чтобы минимизировать затраты на перевозку продукции от заводов-производителей на склады. Зададим следующие исходные условия. Предположим, ЧТО Х ij - объем продукции, который необходимо перевезти из i-го завода на j-й состав; с - - стоимость перевозки единицы продукции с i-го завода на j-й состав. Тогда целевая функция задачи - стоимость перевозки, будет иметь следующий вид:

Рис. 7.3.

Условие того, что вся продукция будет транспортироваться с каждого завода:

Данные равенства можно записать в краткой форме, а именно:

Условие заполнения складов имеет следующий вид: причем

Данная модель может быть описана с помощью сети, если предположить, что узлами сети есть заводы и склады, а дугами - дороги для перевозки груза (рис. 7.3). Сформулирована транспортная задача является частным случаем задачи поиска потока минимальной стоимости в пределах сети.

Сетевые задачи применяют при проектировании и усовершенствованные больших и сложных систем, а также при условии поиска путей их наиболее рационального использования. В первую очередь, это связано с тем, что с помощью сетей можно достаточно просто построить модель системы. Последнее базируется на идее критического пути (метод СРМ) и оценке и средствах наблюдения (например, система PERT- Program Evalution Research Task).

Кроме того, сети позволяют осуществить :

Формализацию модели сложной системы как совокупности простых систем (в этом случае логистической системы как совокупности ее подсистем и звеньев - закупки, складов, транспортировки, запасов, производства, распределения и сбыта);

Составление формальных процедур для определения качественных характеристик системы;

Определение механизма взаимодействия компонентов управляющей системы с целью описания последней в терминах ее основных характеристик;

Определение данных, необходимых для исследования логистической системы и ее основных подсистем;

Начальное исследование управляющей системы, составление предварительного расписания работы ее компонентов.

Основное преимущество сетевого подхода заключается в том, что он может быть успешно применен к решению практически любых задач, когда можно точно построить сетевую модель.

Обобщенная характеристика математических моделей, классифицируемых по способу описания объекта, приведена в табл. 7.3. В таблице указаны наиболее подходящие области применения данных моделей с предварительно обозначенной точностью получаемых оценок. Данная информация полезна логистам на этапе построения моделей или выбора последних для решения возникшей проблемы.

По характеру отображаемых свойств объекта модели классифицируются на структурные и функциональные, которые в совокупности отражают взаимосвязь и взаимное влияние отдельных элементов на процессы, протекающие в объекте при его функционировании или изготовлении.

Структурные модели предназначены для отображения структурных свойств объекта состава, взаимосвязи и взаимного расположения, а также формы компонентов.

Функциональные модели предназначены в большей степени для отображения процессов, протекающих в объекте при его функционировании или изготовлении, и, как правило, содержат алгоритмы, связывающие фазовые переменные, внутренние, внешние или выходные параметры.

Таблица 7.3

Характерные черты математических моделей

вид модели	Наиболее пригодна область использования модели	Относительная точность расчета,%
алгебраические	Общие операционные проблемы: анализ процесса затраты - прибыль и т.п.
Модель линейного программирования	Планирование производства, распределение рабочей силы, анализ размещения, смешивания ингредиентов в продуктах питания и др.
Сетевые (поточные)	Предварительно: исследовательские и конструкторские работы, разработка производственных проектов
Вероятностно-статистические:
Модели теории очередей	Оценка систем сервиса
Модели запасов	Управление активами фирмы, предприятия
Статистические	В различных сферах с достаточной долей неопределенности
Регрессионно-корреляционные	В сферах управления, производства, анализ спроса и др. |

По способу формализации объекта при сложности имеющихся ситуаций возникает необходимость в упрощенном их описании с помощью аналитических и алгоритмических моделей, должным образом

"Абстрагируют" избранные "существенные" свойства объектов и ситуаций. Компьютерная имитация реальных объектов - это ценный инструмент для анализа сложных систем сервиса, политики обслуживания и инвестиционного выбора.

Распределение объектов на иерархические уровни приводит к определенным уровней моделирования, иерархия которых определяется как сложностью объектов, так и возможностью средств управления. Поэтому, согласно принадлежности к иерархического уровня, математические модели делятся на микро-, макро- и метамодели. Отличие данных моделей заключается в том, что на более высоком уровне иерархии компоненты модели принимают вид довольно сложных совокупностей элементов предыдущего уровня. Этими же качествами определяется и разделение моделей по степени масштабности и сложности описания объекта.

Приведенная классификация моделей призвана помочь логистам в более оперативном и правильном принятии решений в целях осуществления миссии организации.

К классификации математических моделей также можно подойти с разных точек зрения, положив в основу классификации различные принципы (см. табл. 20.1).

по отраслям наук : математические модели в физике, биологии, социологии и т.д. Такая классификация естественна для специалиста в ка-кой-то одной науке, предметной области .

Можно классифицировать модели по применяемому математическому аппарату : модели, основанные на использовании обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, вероятностно-статистических методов, дискретных алгебраических преобразований и т.д. Подобная классификация удобна для специалиста в области математического моделирования .

В зависимости от целей моделирования можно привести следующую классификацию :

· дескриптивные (описательные) модели;

· оптимизационные однокритериальные модели;

· оптимизационные многокритериальные модели;

· игровые модели;

· имитационные модели.

Например, при моделировании движения кометы, в Солнечной системе, описывается (предсказывается) траектория ее полета, расстояние, на котором она пройдет от Земли и т.д., т. е. ставятся чисто описательные цели. У исследователя нет возможности повлиять на движение кометы, что-то изменить.

В других случаях можно воздействовать на процессы, пытаясь добиться какой-то цели.

Например, меняя ассортимент продукции, которая выпускается предприятием и объем выпуска продукции каждого вида можно найти такие значения, при которых достигается максимальная прибыль, т.е. определяется оптимальный план выпуска продукции по критерию максимизации прибыли.

Часто приходится находить оптимальное решение задачи по нескольким критериям сразу, причем цели могут быть весьма противоречивыми.

Например, зная цены на продукты и потребность человека в пище, определить рацион питания больших групп людей (в армии, летнем лагере и др.) наиболее дешевый и наиболее калорийный. Очевидно, что эти цели, могут противоречить друг другу и необходимо найти компромиссное решение, удовлетворяющее в определенной степени всем критериям.

Игровые модели могут иметь отношение не только к детским играм (в том числе и компьютерным), но и к вещам весьма серьезным.

Например, полководец перед сражением в условиях наличия неполной информации о противостоящей армии должен разработать план: в каком порядке вводить в бой те или иные части и т.д., учитывая и возможную реакцию противника.

Наконец, бывает, что модель в большой мере подражает реальному процессу, т.е. имитирует его.

Например, моделируя изменение (динамику) численности микроорганизмов в колонии, можно рассматривать много отдельных объектов и следить за судьбой каждого из них, ставя определенные условия для его выживания, размножения и т.д. При этом явное математическое описание процесса может не использоваться, заменяясь некоторыми условиями (например, по истечении заданного отрезка времени микроорганизм делится на две части, а другого отрезка - погибает).

В настоящее время моделирование широко используется в сфере управления различными системами, где основными являются процессы принятия решений на основе получаемой информации . Моделирование применяется при исследовании, проектировании, внедрении вычислительных систем (ВС) и автоматизированных систем управления (АСУ).

Выбор математической модели зависит от этапа разработки системы. На этапах об-следования объекта управления (например, промышленного предприятия) и разработки технического задания на проектирование ВС, АСУ строятся описательные модели и преследуют цель наиболее полно представить в компактной форме информацию об объекте, необходимую разработчику системы.

На этапе разработки технического проекта ВС, АСУ моделирование служит для решения задачи проектирования, т.е. выбора оптимального варианта по определенному критерию или совокупности критериев при заданных ограничениях из множества допустимых (построение однокритериальных и многокритериальных оптимизационных моделей).

На этапе внедрения и эксплуатации ВС, АСУ строятся имитационные модели для проигрывания возможных ситуаций для принятия обоснованных и перспективных решений по управлению объектом. Игровые и имитационные модели также широко применяют при обучении и тренировке персонала.

В зависимости от характера изучаемых процессов , протекающих в системе (объекте) все виды моделей могут быть разделены на детерминированные и стохастические, статические и динамические, дискретные, непрерывные и дискретно-непрерывные ,,,.

Детерминированная модель отображает детерминированные процессы, т.е. процессы, в которых предполагается отсутствие всяких случайных воздействий. В детерминированных моделях входные параметры поддаются измерению однозначно и с любой степенью точности, т.е. являются детерминированными величинами. Соответственно, процесс эволюции такой системы детерминирован.

Например, детерминированные модели используются в физике (модель движения автомобиля при равноускоренном движении: задавая начальную скорость и ускорение можно точно рассчитать путь, пройденный автомобилем с момента начала движения в идеальных условиях), для описания движения небесных тел в астрономии также используют детерминированные модели.

Стохастические (теоретико-вероятностные) модели используются для отображения вероятностных процессов и событий. В этом случае анализируется ряд реализаций случайного процесса, и оцениваются средние характеристики. В стохастических моделях значения входных параметров (переменных) известны лишь с определенной степенью вероятности, т.е. эти параметры являются стохастическими; соответственно, случайным будет и процесс эволюции системы.

Например, модель, описывающая изменение температуры воздуха в течение года. Точно предсказать температуру воздуха не будущий период невозможно, задается только диапазон изменения температуры и вероятность того, что истинная температура воздуха попадет в этот диапазон.

Стохастические модели применяется для исследования системы, состояние которой зависит не только от контролируемых, но и от неконтролируемых воздействий или в ней самой есть источник случайности. К стохастическим системам относятся все системы, которые включают человека, например, заводы, аэропорты, вычислительные системы и сети, магазины, предприятия бытового обслуживания и т.п.

Статические модели служат для описания поведения объекта в какой-либо момент времени, а динамические модели отражают поведение объекта во времени.

Например, вероятностно-статистическая модель, описывающая взаимосвязи между годовыми показателями деятельности (прибыль, объем производства, фонд заработной платы и т.д.) предприятий торговли г. Новосибирска за прошедший год – статическая. В качестве исходных данных при моделировании используются годовые показатели за один год, на-пример, по 100 предприятиям торговли.

Если решается та же задача, но изучаются показатели в динамике за несколько лет, то для описания взаимосвязей необходимо применять динамические модели. В математическом описании динамической модели всегда присутствует переменная время, при математическом описании статической модели время либо не вводится, либо зафиксировано на определенном уровне.

Дискретные модели служат для описания процессов, которые предполагаются дискретными, соответственно непрерывные модели позволяют отразить непрерывные процессы в системах, а дискретно-непрерывное моделирование используется для случаев, когда хотят выделить наличие как дискретных, так и непрерывных процессов.

Например, моделируется работа дифференцирующего фильтра: каждый такт времени через равные промежутки подается входной сигнал X(t) на выходе снимается значение производной X"(t) . В данном случае входной и выходной сигналы – дискретны по времени и соответственно дискретна модель.

Пример непрерывной модели по времени – имитационная модель, описывающая процесс обработки деталей на производственном участке цеха в течение рабочей смены. На вход модели поступают заявки (детали) через случайные интервалы времени, интервал обработки детали также задан случайно. На выходе модели – оценка среднего времени обработки детали, оценка среднего времени ожидания в очереди на обработку, вероятность простоя оборудования и т.п. Работа системы моделируется непрерывно в течение заданного промежутка времени (рабочая смена), т.е. в любой момент времени может поступить деталь на обработку или завершиться обработка детали.

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

АННОТАЦИЯ

В данной курсовой работе будут рассмотрены виды математических моделей, их классификация, основные типы математических моделей, их схемы. Будут приведены примеры построения математических моделей на нескольких примерах. Эта работа поможет студентам разобраться во всем многообразии видов и типов математических моделей, понять по какому принципу можно классифицировать математические модели, от чего зависит выбор той или иной математической модели. Здесь мы узнаем какие бывают схемы математических моделей и каковы их особенности.

ABSTRACT

In given term paper will are considered types of the mathematical models, their categorization. The Main types of the mathematical models, their schemes. Will cite an instance buildings of the mathematical models on several examples.

Введение

1. Моделирование

1.1 Цели и задачи моделирования

1.2 Требования к модели

2. Классификация моделей

3. Математическое моделирование

3.1 Непрерывно детерминированные модели (Д - схемы)

3.2 Дискретно-детерминированные модели (F-схемы)

3.3 Методы теории массового обслуживания

4. Выбор математической модели

4.1 Сопоставление методов построения математических моделей

4.2 Достоверность и простота модели

4.3 Проверка адекватности и идентификация модели

4.4 Выбор математической модели

5. Примеры составления математических моделей

Заключение

Список источников информации

ВВЕДЕНИЕ

На современном этапе экономического и социального развития республики предъявляются высокие требования к уровню экономической работы на всех уровнях. Сегодня особенно необходимы качественные сдвиги в экономике, существенное повышение эффективности работы всех звеньев хозяйственной системы: предприятий, объединений, отраслей. Особую важность, в условиях расширяющихся прав предприятий, в области производственно-хозяйственной деятельности, их самостоятельности в принятии управленческих решений, приобретает глубокое знание специалистами новейших достижений экономической науки, методов математического моделирования и прогнозирования экономических процессов на основе информационных технологий оптимальных решений. Эти обстоятельства выдвигают повышенные требования к качеству подготовки специалистов, которые должны владеть новейшими достижениями наук и уметь, используя их богатый арсенал методов, находить самые эффективные управленческие решения, а, это, в свою очередь, определяет роль и место математических методов оптимизации в учебном процессе. моделирование обслуживание детерминированный

Методы математического моделирования, являясь мощным инструментом исследований экономических процессов, играет весьма важную роль в анализе и синтезе экономического развития, определение обеспечивает многоуровневую оптимизацию, схватывающую взаимосвязи отраслей, регионов и предприятий.

В науке, технике и экономике используются модели, которые общепринятым, формальным способом описывают характерные особенности систем и позволяют осуществлять достаточно надежное прогнозирование их поведение. Простейшими моделями могут выступать таблицы или графики, связывающие величины воздействия на систему с величинами, отражающими ее реакцию на эти воздействия. Более высокий уровень моделей - уравнения, отражающие подобную связь (алгебраические, дифференциальные, интегральные и пр.). свойства сложной системы отражают совокупностью различных уравнений. Такие модели называют математическими и описывают классы систем. Независимо от способа создания математической модели, она всегда приближенно отражает исследуемую систему. Это связано с неполнотой наших знаний о природе протекающих в системе процессов, с невозможностью учесть все процессы и их особенности (чрезмерно громоздкая математическая модель), с неточным представлением данных о системе и ее элементах. Имея математическую модель системы, можно проводить прогнозирование ее поведения в различных ситуациях (проводить математическое моделирование системы).

1. МОДЕЛИРОВАНИЕ

Моделировaние - это изучение объектa путем построения и исследования его модели, осуществляемое с определенной целью и состоит в зaмене экспериментa с оригиналом экспериментом на модели. Модель должна строится так, чтобы она наиболее полно воспроизводила те кaчествa oбъектa, которые необходимо изучить в соответствии с поставленной целью. Во всех отношениях модель должна быть проще объекта и удобнее его для изучения. Таким образом, для одного и того же объекта могут существовать различные модели, классы моделей, соответствующие различным целям его изучения. Необходимым условием моделирования является подобие объекта и его модели. Т.е. моделирование - это замещение одного объекта (оригинала) другим (моделью) и фиксация и изучение свойств модели. Замещение производится с целью упрощения , удешевления, ускорения изучения свойств оригинала.

В общем случае объектом-оригиналом может быть естественная или искусственная, реальная или воображаемая система. Она имеет множество параметров и характеризуется определёнными свойствами. Количественной мерой свойств системы служит множество характеристик, система проявляет свои свойства под влиянием внешних воздействий. От специaлистa, зaнимaющегося построением моделей, требуются следующие основные кaчествa:

o четкое представление о сущности физико-химических явлений, протекающих в объекте;

o умение мaтемaтически описывать протекающие процессы и применять методы моделирования;

o быть в состоянии обеспечить получение на модели содержательных результатов.

1.1 Цели и задачи моделирования

Основные цели и задачи моделирования сводятся к следующему:

1. Оптимальное проектирование новых и интенсификация действующих технологических процессов.

2. Контроль за ходом процесса, получение необходимой информации о нем и обрaботкa полученной информации с целью управления ходом технологического процесса.

3. Решение зaдaч исследования объектов, где невозможно проводить активные эксперименты - режимы работы реакторов, траектории космических объектов и т.д.

4. Мaксимaльное ускорение переносa результaтов лaборaторных исследовaний в промышленные мaсштaбы.

1.2 Требования к модели

1. Зaтрaты нa создaние модели должны быть знaчительно меньше зaтрaт нa создaние оригинaлa.

2. Должны быть четко определены прaвилa интерпретaции результaтов вычислительного экспериментa.

3. Основное требовaние - модель должнa быть существенной. Это требовaние зaключaется в том, что модель должнa отрaжaть необходимые, существенные для решения конкретной зaдaчи свойствa объектa. Для одного и того же объектa сложно создaть обобщенную модель, отрaжaющую все его свойствa. Поэтому вaжно обеспечить существенность модели.

Моделирование целесообразно, когда у модели отсутствуют те признаки оригинала, которые препятствуют его исследованию.

Теория моделирования -- взаимосвязанная совокупность положений, определений, методов и средств создания моделей. Сами модели являются предметом теории моделирования.

Теория моделирования является основной составляющей общей теории систем - системологии, где в качестве главного принципа постулируются осуществимые модели: система представима конечным множеством моделей, каждая из которых отражает определённую грань её сущности.

2 . КЛАССИФИКАЦИЯ МОДЕЛЕЙ

Клaссификaцию моделей можно проводить по разным типам признаков:

- по способу познания: научно-технические, художественные, житейские;

- по природе моделей: предметные (физические / мaтериaльные), знаковые (мысленные).

Рис.1 Классификация моделей по природе

- по отношению ко времени различают статические и динамические модели;

- по характеру зависимости выходных параметров от входных модели делятся на детерминированные и стохастические.

Мaтериaльные модели - уменьшенное (увеличенное) отражение оригинaлa с сохранением физической сущности (реaктор - пробиркa). Мысленная модель - отображение оригинaлa , отрaжaющaя существенные черты и возникaющaя в сознaнии человекa в процессе познaния. Обрaзные модели носят описaтельный хaрaктер. Знaковые модели - являются мaтемaтическими описaниями процессов, явлений, объектов и обычно нaзывaются мaтемaтическими моделями. Знaковые модели могут тaкже включaть в себя схемы и чертежи.

В иды моделей по отношению ко времени и по характеру выходных параметров

Рис.2.

Физические модели. В основу классификации положена степень абстрагирования модели от оригинала. Предварительно все модели можно подразделить на 2 группы -- физические и абстрактные (математические).

Физической моделью обычно называют систему, эквивалентную или подобную оригиналу, но возможно имеющую другую физическую природу. Виды физических моделей:

натуральные;

квазинатуральные;

масштабные;

аналоговые.

Натуральные модели -- это реальные исследуемые системы (макеты, опытные образцы). Имеют полную адекватность (соответствия) с системой оригиналом, но дороги.

Квазинатуральные модели -- совокупность натуральных и математических моделей. Этот вид используется тогда, когда модель части системы не может быть математической из-за сложности её описания (модель человека оператора) или когда часть системы должна быть исследована во взаимодействии с другими частями, но их ещё не существует или их включение очень дорого (вычислительные полигоны, автоматизированные системы управления).

Масштабная модель -- это система той же физической природы, что и оригинал, но отличается от него масштабами. Методологической основой масштабного моделирования является теория подобия. При проектировании вычислительных систем масштабные модели могут использоваться для анализа вариантов компоновочных решений.

Аналоговыми моделями называют системы, имеющие физическую природу, отличающуюся от оригинала, но сходные с оригиналом процессы функционирования. Для создания аналоговой модели требуется наличие математического описания изучаемой системы. В качестве аналоговых моделей используются механические, гидравлические, пневматические и электрические системы. Аналоговое моделирование использует при исследовании средства вычислительной техники на уровне логических элементов и электрических цепей, а так же на системном уровне, когда функционирование системы описывается например, дифференциальными или алгебраическими уравнениями.

Математические модели представляют собой формализованное представление системы с помощью абстрактного языка, с помощью математических соотношений, отражающих процесс функционирования системы. Для составления математических моделей можно использовать любые математические средства -- алгебраическое, дифференциальное, интегральное исчисления, теорию множеств, теорию алгоритмов и т.д. По существу вся математика создана для составления и исследования моделей объектов и процессов.

К средствам абстрактного описания систем относятся также языки химических формул, схем, чертежей, карт, диаграмм и т.п. Выбор вида модели определяется особенностями изучаемой системы и целями моделирования, т.к. исследование модели позволяет получить ответы на определённую группу вопросов. Для получения другой информации может потребоваться модель другого вида. Математическое модели можно классифицировать на детерминированные и вероятностные, аналитические, численные и имитационные.

Аналитической моделью называется такое формализованное описание системы, которое позволяет получить решение уравнения в явном виде, используя известный математический аппарат.

Численная модель характеризуется зависимостью (1.2) такого вида, который допускает только частные решения для конкретных начальных условий и количественных параметров моделей.

Имитационная модель -- это совокупность описания системы и внешних воздействий, алгоритмов функционирования системы или правил изменения состояния системы под влиянием внешних и внутренних возмущений. Эти алгоритмы и правила не дают возможности использования имеющихся математических методов аналитического и численного решения, но позволяют имитировать процесс функционирования системы и производить вычисления интересующих характеристик. Имитационные модели могут быть созданы для гораздо более широкого класса объектов и процессов, чем аналитические и численные. Поскольку для реализации имитационных моделей служат ВС, средствами формализованного описания ИМ служат универсальные и специальные алгоритмические языки. ИМ в наибольшей степени подходят для исследования ВС на системном уровне.

3 . МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Это вaжнейший метод современного нaучного исследовaния, основной aппaрaт системного aнaлизa. Мaтемaтическое моделировaние - это изучение поведения объектa в тех или иных условиях путем решения урaвнений его мaтемaтичекой модели. В химической технологии мaтемaтическое моделировaние применяют прaктически нa всех уровнях исследовaния, рaзрaботки и внедрения. Дaнный метод бaзируется нa мaтемaтическом подобии. У мaтемaтически подобных объектов процессы облaдaют рaзличной физической природой, но описывaются идентичными урaвнениями.

Нa первых порaх своего рaзвития мaтемaтическое моделировaние нaзывaлось aнaлоговым. Более того, использовaние методa aнaлогии привело к появлению aнaлоговых вычислительных мaшин - AВМ. Это электронные устройствa, состоящие из интегрaторов, дифференцирующих устройств, суммaторов и усилителей. Нa AВМ моделируются физические явления, которые aнaлогичны эффектaм электрической природы. По срaвнению с физическим мaтемaтическое моделировaние - более универсaльный метод.

Математическое моделирование:

- позволяет осуществить с помощью одного устройствa (ЭВМ) решение целого клaссa зaдaч, имеющих одинaковое мaтемaтическое описaние;

- обеспечивaет простоту переходa от одной зaдaчи к другой, позволяет вводить переменные пaрaметры, возмущения и рaзличные нaчaльные условия;

- дaет возможность проводить моделировaние по чaстям ("элементaрным процессaм"), что особенно существенно при исследовaнии сложных объектов химической технологии;

- экономичнее методa физического моделировaния кaк по зaтрaтaм, тaк и по стоимости.

Исходной информацией при построении математической модели процессов функционирования систем служат данные о назначении и условиях работы исследуемой (проектируемой) системы S. Эта информация определяет основную цель моделирования, требования к математической модели, уровень абстрагирования, выбор математической схемы моделирования.

Понятие математическая схема позволяет рассматривать математику не как метод расчёта, а как метод мышления, средства формулирования понятий, что является наиболее важным при переходе от словесного описания к формализованному представлению процесса её функционирования в виде некоторой математической модели.

При пользовании математической схемой в первую очередь исследователя системы должен интересовать вопрос об адекватности отображения в виде конкретных схем реальных процессов в исследуемой системе, а не возможность получения ответа (результата решения) на конкретный вопрос исследования.

Математическую схему можно определить как звено при переходе от содержательного к формализованному описанию процесса функционирования системы с учётом воздействия внешней среды. Т.е. имеет место цепочка: описательная модель -- математическая схема -- имитационная модель.

В качестве детерминированных моделей, когда при исследовании случайный факт не учитывается, для представления систем, функционирующих в непрерывном времени, используются дифференциальные, интегральные и др. уравнения, а для представления систем, функционирующих в дискретном времени -- конечные автоматы и конечно разностные схемы.

В начале стохастических моделей (при учёте случайного фактора) для представления систем с дискретным временем используются вероятностные автоматы, а для представления систем с непрерывным временем -- системы массового обслуживания (СМО). Большое практическое значение при исследовании сложных индивидуальных управленческих систем, к которым относятся автоматизированные системы управления, имеют так называемые агрегативные модели.

Aгрегативные модели (системы) позволяют описать широкий круг объектов исследования с отображением системного характера этих объектов. Именно при агрегативном описании сложный объект расчленяется на конечное число частей (подсистем), сохраняя при этом связи, обеспечивая взаимодействие частей.

3 .1 Непрерывно детерминированные м о дели (Д - схемы)

Рассмотрим особенности непрерывно детерминированного подхода на примере, используя в качестве математической модели дифференциальные уравнения.

Дифференциальными уравнениями называются такие уравнения, в которых неизвестными будут функции одной переменной или нескольких переменных, причём в уравнение входят не только их функции но их производные различных порядков.

Если неизвестные - функции многих переменных, то уравнения называются -- уравнения в частных производных. Если неизвестные функции одной независимой переменной, то имеют место обыкновенные дифференциальные уравнения.

Математическое соотношение для детерминированных систем в общем виде:

Например, процесс малых колебаний маятника описан обыкновенными дифференциальным уравнением где m 1 , l 1 - масса, длина подвески маятника, - угол отклонения маятника от положения равновесия. Из этого уравнения можно найти оценки интересующих характеристик, например период колебаний

Дифференциальные уравнения, Д - схемы являются математическим аппаратом теории систем автоматического регулирования, управления.

При проектировании и эксплуатации систем автоматического регулирования (САУ) необходимо выбрать такие параметры системы, которые бы обеспечивали требуемую точность управления.

Следует отметить, что часто используемые в САУ системы дифференциальных уравнений определяются путём линеаризацией управления объекта (системы), более сложного вида, имеющего нелинейности:

3 .2 Дискретно - детерминированные модели ( F -схемы)

Дискретно - детерминированные модели (ДДМ) являются предметом рассмотрения теории автоматов (ТА). ТА - раздел теоретической кибернетики, изучающей устройства, перерабатывающие дискретную информацию и меняющего свои внутренние состояния лишь в допустимые моменты времени.

Конечный автомат имеет множество внутренних состояний и входных сигналов, являющихся конечными множествами. Автомат задаётся F- схемой:

F=,

где z,x,y - соответственно конечные множества входных, выходных сигналов (алфавитов) и конечное множество внутренних состояний (алфавита). z 0 Z - начальное состояние; (z,x) - функция переходов; (z,x) - функция выхода. Автомат функционирует в дискретном автоматном времени, моментами которого являются такты, т.е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного, выходного сигнала и внутреннего состояния. Абстрактный автомат имеет один входной и один выходной каналы.

В момент t, будучи в состоянии z(t), автомат способен воспринять сигнал x(t) и выдать сигнал y(t)=, переходя в состояние z(t+1)=, z(t)Z; y(t)Y; x(t)X. Абстрактный КА в начальном состоянии z 0 принимая сигналы x(0), x(1), x(2) … выдаёт сигналы y(0), y(1), y(2)… (выходное слово).

Существуют F- автомат 1-ого рода (Миля), функционирующий по схеме:

z(t+1)= , t=0,1,2…(1)

y(t)=, t=0,1,2…(2)

автомат 2-ого рода:

z(t+1)= , t=0,1,2…(3)

y(t)=, t=1,2,3…(4)

Автомат 2-ого рода, для которого y(t)=, t=0,1,2,…(5)

т.е. функция выходов не зависит от входной переменной x(t), называется автоматом Мура.

Т.о. уравнения 1-5 полностью задающие F- автомат, являются частным случаем уравнения

(6)

где - вектор состояния, - вектор независимых входных переменных, - вектор воздействий внешней среды, - вектор собственных внутренних параметров системы, - вектор начального состояния, t - время; и уравнение,(7)

когда система S - деноминированная и на её вход поступает дискретный сигнал x.

По числу состояний конечные автоматы бывают с памятью и без памяти. Автоматы с памятью имеют более одного состояния, а автоматы без памяти (комбинационные или логические схемы) обладают лишь одним состоянием. При этом согласно (2), работа комбинационной схемы заключается в том, что она ставит в соответствие каждому входному сигналу x(t) определённый выходной сигнал y(t), т.е. реализует логическую функцию вида:

y(t)=, t=0,1,2,…

Эта функция называется булевой, если алфавиты X и Y, которым принадлежат значения сигналов x и y состоят из 2-х букв.

По характеру отсчёта времени (дискретному) F- автоматы делятся на синхронные и асинхронные. В синхронных автоматах моменты времени, в которые автомат "считывает" входные сигналы, определяются принудительно синхронизирующими сигналами. Реакция автомата на каждое значение входного сигнала заканчивается за один такт синхронизации. Асинхронный F- автомат считывает входной сигнал непрерывно и поэтому, реагируя на достаточно длинный водной сигнал постоянной величины x, он может, как это следует из 1-5, несколько раз изменить своё состояние, выдавая соответствующее число выходных сигналов, пока не перейдёт в устойчивое.

Для задания F- автомата необходимо описать все элементы множества F=, т.е. входной, внутренний и выходной алфавиты, а также функции переходов и выходов. Для задания работы F- автоматов наиболее часто используются табличный, графический и матричный способ.

В табличном способе задания используется таблицы переходов и выходов, строки которых соответствуют входным сигналам автомата, а столбцы - его состояниям. При этом обычно 1-ый столбец слева соответствует начальному состоянию z 0 . На пересечении i-ой строки и j-ого столбца таблицы переходов помещается соответствующее значение (z k ,x i) функции переходов, а в таблице выходов - (z k , x i) функции выходов. Для F- автомата Мура обе таблицы можно совместить, получив т.н. отмеченную таблицу переходов, в которой над каждым состоянием z k автомата, обозначающим столбец таблицы, стоит соответствующий этому состоянию, согласно (5), выходной сигнал (z i).

Описание работы F- автомата Мили таблицами переходов и выходов иллюстрируется таблицей 3.1., а описание F- автомата Мура - таблицей переходов 3.2..

Таблица 3.1. Описание работы автомата Мили

Переходы
…………………………………………………………
…………………………………………………………

Таблица 3.2. Описание работы автомата Мура

……………………………………………………

Примеры табличного способа задания F- автомата Мили F1 с тремя состояниями, двумя входными и двумя выходными сигналами приведены в таблице 3.3, а для F- автомата Мура F2 - в таблице 3.4.

Таблица 3.3. Способ задания автомата Мили с тремя состояниями

Переходы

Таблица 3.4. Способ задания автомата Мура с тремя состояниями

При другом способе задания конечного автомата используется понятие направленного графа. Граф автомата представляет собой набор вершин, соответствующих различным состояниям автомата и соединяющих вершин дуг графа, соответствующих тем или иным переходам автомата. Если входной сигнал x k вызывает переход из состояния z i в состояние z j , то на графе автомата дуга, соединяющая вершину z i с вершиной z j обозначается x k . Для того, чтобы задать функцию переходов, дуги графа необходимо отметить соответствующими выходными сигналами. Для автоматов Мили эта разметка производиться так: если входной сигнал x k действует на состояние z i , то согласно сказанному получается дуга, исходящая из z i и помеченная x k ; эту дугу дополнительно отмечают выходным сигналом y=(z i , x k). Для автомата Мура аналогичная разметка графа такова: если входной сигнал x k , действуя на некоторое состояние автомата, вызывает переход в состояние z j , то дугу, направленную в z j и помеченную x k , дополнительно отмечают выходным сигналом y=(z j , x k). На рис. 3 приведены заданные ранее таблицами F- автоматы Мили F1 и Мура F2 соответственно.

Рис. 3 . Графы автоматов Мили (а) и Мура (б)

При решении задач моделирования часто более удобной формой является матричное задание конечного автомата. При этом матрица соединений автомата есть квадратная матрица С=|| c ij ||, строки которой соответствуют исходным состояниям, а столбцы - состояниям перехода. Элемент c ij =x k /y S в случае автомата Мили соответствует входному сигналу x k , вызывающему переход из состояния z i в состояние z j и выходному сигналу y S , выдаваемому при этом переходе. Для автомата Мили F1, рассмотренного выше, матрица соединений имеет вид:

Если переход из состояния z i в состояние z j происходит под действием нескольких сигналов, элемент матрицы c ij представляет собой множество пар "вход/выход" для этого перехода, соединённых знаком дизъюнкции.

Для F- автомата Мура элемент c ij равен множеству входных сигналов на переходе (z i z j), а выход описывается вектором выходов:

i-ая компонента которого выходной сигнал, отмечающий состояние z i

Пример. Для рассмотренного ранее автомата Мура F2 запишем матрицу состояний и вектор выходов:

;

Для детерминированных автоматов переходы однозначны. Применительно к графическому способу задания F- автомата это означает, что в графе F- автомата из любой вершины не могут выходить 2 и более ребра, отмеченные одним и тем же входным сигналом. Аналогично этому в матрице соединений автомата С в каждой строке любой входной сигнал не должен встречаться более одного раза.

Рассмотрим вид таблицы переходов и графа асинхронного конечного автомата. Для F- автомата состояние z k называется устойчивым, если для любого входа x i X, для которого (z k ,x i)=z k имеет место (z k x i)=y k . Т.о. F- автомат называется асинхронным, если каждое его состояние z k Z устойчиво.

На практике всегда автоматы являются асинхронными, а устойчивость их состояний обеспечивается тем или иным способом, например, введением сигналов синхронизации. На уровне абстрактной теории удобно часто оперировать с синхронными конечными автоматами.

Пример. Рассмотрим асинхронный F- автомат Мура, который описан в табл. 3.5 и приведён на рис. 4.

Таблица 3.5. Асинхронный автомат Мура

Рис. 4 . Граф асинхронного автомата Мура

Если в таблице переходов асинхронного автомата некоторое состояние z k стоит на пересечении строки x S и столбца z S (Sk), то это состояние z k обязательно должно встретиться в этой же строке в столбце z k .

С помощью F-схем описываются узлы и элементы электронных вычислительных систем, устройства контроля, регулирования и управления, системы временной и пространственной коммутации в технике обмена информацией. Широта применения F-схем не означает их универсальность. Этот подход непригоден для описания процессов принятия решений, процессов в динамических системах с наличием переходных процессов и стохастических элементов.

3.3 Непрерывно-стохастические модели (Q - схемы)

К ним относятся системы массового обслуживания (англ. queuing system), которые называют Q- схемами.

Предмет теории массового обслуживания -- системы массового обслуживания (СМО) и сети массового обслуживания. Под СМО понимают динамическую систему, предназначенную для эффективного обслуживания случайного потока заявок при ограниченных ресурсах системы. Обобщённая структура СМО приведена на рисунке 5.

Рис. 5 . Схема СМО

Поступающие на вход СМО однородные заявки в зависимости от порождающей причины делятся на типы, интенсивность потока заявок типа i (i=1…M) обозначено i . Совокупность заявок всех типов - входящий поток СМО.

Обслуживание заявок выполняется m каналами. Различают универсальные и специализированные каналы обслуживания. Для универсального канала типа j считается известными функции распределения F ji () длительности обслуживания заявок произвольного типа. Для специализированных каналов функции распределения длительности обслуживания каналов заявок некоторых типов являются неопределёнными, назначение этих заявок на данный канал.

В качестве процесса обслуживания могут быть представлены различные по своей физической природе процессы функционирования экономических, производственных, технических и других систем, например, потоки поставок продукции некоторому предприятию, потоки деталей и комплектующих изделий на сборочном конвейере цеха, заявки на обработку информации электронных вычислительных систем от удалённых терминалов и т.д. При этом характерным для работы таких объектов является случайное поведение заявок (требований) на обслуживание и завершение обслуживания в случайные моменты времени.

Q - схемы можно исследовать аналитически и имитационными моделями. Последнее обеспечивает большую универсальность.

Рассмотрим понятие массового обслуживания.

В любом элементарном акте обслуживания можно выделить две основные составляющие: ожидание обслуживания заявкой и собственно обслуживание заявки. Это можно отобразить в виде некоторого i-ого прибора обслуживания П i , состоящего из накопителя заявок, в котором может находится одновременно l i =0…L i H заявок, где L i H - ёмкость i-ого накопителя, и канала обслуживания заявок, k i .

Рис. 6 . Схема прибора СМО

На каждый элемент прибора обслуживания П i поступают потоки событий: в накопитель H i поток заявок w i , на канал k i - поток обслуживания u i .

Потоком событий (ПС) называется последовательность событий, происходящих одно за другим в какие-то случайные моменты времени. Различают потоки однородных и неоднородных событий. Однородный ПС (ОПС) характеризуется только моментами поступления этих событий (вызывающими моментами) и задаётся последовательностью {t n }={0t 1 t 2 …t n …}, где t n - момент поступления n- ого события - неотрицательное вещественное число. ОПС может быть также задан в виде последовательности промежутков времени между n-ым и n-1-ым событиями { n }.

Неоднородным ПС называется последовательность {t n , f n } , где t n - вызывающие моменты; f n - набор признаков события. Например, может быть задана принадлежность к тому или иному источнику заявок, наличие приоритета, возможность обслуживания тем или иным типом канала и т.п.

Рассмотрим ОПС, для которого i { n }- случайные величины, независимые между собой. Тогда ПС называется потоком с ограниченным последействием.

ПС называется ординарным, если вероятность того, что на малый интервал времени t, примыкающий к моменту времени t попадает больше одного события Р 1 (t, t) пренебрежительно мала.

Если для любого интервала t событие P 0 (t, t) + P 1 (t, t) + Р 1 (t, t)=1, P 1 (t, t) - вероятность попадания на интервал t ровно одного события. Как сумма вероятностей событий, образующих полную группу и несовместных, то для ординарного потока событий P 0 (t, t) + P 1 (t, t) 1, Р 1 (t, t)=(t), где (t)- величина, порядок малости который выше, чем t, т.е. lim((t))=0 при t0.

Стационарным ПС называется поток, для которого вероятность появления того или иного числа событий на интервале времени зависит от длины этого участка и не зависит от того, где на оси времени 0 - t взят этот участок. Для ОПС справедливо 0*P 0 (t, t) + 1*P 1 (t, t)= P 1 (t, t) - среднее число событий на интервале t. Среднее число событий, наступающих на участке t в единицу времени составляет P 1 (t, t)/t. Рассмотрим предел этого выражения при t0

lim P 1 (t, t)/t=(t)*(1/един.вр.).

Если этот предел существует, то он называется интенсивностью (плотностью) ОПС. Для стандартного ПС (t)==const.

Применительно к элементарному каналу обслуживания k i можно считать что поток заявок w i W, т.е. интервалы времени между моментами появления заявок на входе k i образуют подмножество неуправляемых переменных, а поток обслуживания u i U, т.е. интервалы времени между началом и окончанием обслуживания заявки образуют подмножество управляемых переменных.

Заявки, обслуженные каналом k i и заявки, покинувшие прибор П i по различным причинам не обслуженными, образуют выходной поток y i Y.

Процесс функционирования прибора обслуживания П i можно представить как процесс изменения состояний его элементов во времени Z i (t). Переход в новое состояние для П i означает изменение кол-ва заявок, которые в нём находятся (в канале k i и накопителе H i). Т.о. вектор состояний для П i имеет вид: , где - состояния накопителя, (=0 - накопитель пуст, =1- в накопителе одна заявка…, =- накопитель занят полностью; - состояние канала k i (=0 - канал свободен, =1 канал занят).

Q-схемы реальных объектов образуются композицией многих элементарных приборов обслуживания П i . Если k i различных приборов обслуживания соединены параллельно, то имеет место многоканальное обслуживание (многоканальная Q-схема), а если приборы П i и их параллельные композиции соединены последовательно, то имеет место многофазное обслуживание (многофазная Q-схема).

Т.о. для задания Q-схемы необходимо оператор сопряжения R, отражающий взаимосвязь элементов структуры.

Связи в Q-схеме изображают в виде стрелок (линий потока, отражающих направление движения заявок). Различают разомкнутые и замкнутые Q-схемы. В разомкнутой выходной поток не может снова поступить на какой-либо элемент, т.е. обратная связь отсутствует.

Собственными (внутренними) параметрами Q-схемы будут являться кол-во фаз L Ф, количество каналов в каждой фазе, L kj , j=1… L Ф, количество накопителей каждой фазы L kj , k=1… L Ф, ёмкость i-ого накопителя L i H . Следует отметить, что в теории массового обслуживания в зависимости от ёмкости накопителя применяют следующую терминологию:

системы с потерями (L i H =0, накопитель отсутствует);

системы с ожиданием (L i H);

системы с ограниченной ёмкостью накопителя Н i (смешанные).

Обозначим всю совокупность собственных параметров Q-схемы как подмножество Н.

Для задания Q-схемы также необходимо описать алгоритмы её функционирования, которые определяют правила поведения заявок в различных неоднозначных ситуациях.

В зависимости от места возникновения таких ситуаций различают алгоритмы (дисциплины) ожидания заявок в накопителе Н i и обслуживания заявок каналом k i . Неоднородность потока заявок учитывается с помощью введения класса приоритетов.

В зависимости от динамики приоритетов Q-схемы различают статические и динамические. Статические приоритеты назначаются заранее и не зависят от состояний Q-схемы, т.е. они являются фиксированными в пределах решения конкретной задачи моделирования. Динамические приоритеты возникают при моделировании. Исходя из правил выбора заявок из накопитель Н i на обслуживание каналом k i можно выделить относительные и абсолютные приоритеты. Относительный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель Н, ожидает окончания обслуживания представляющей заявки каналом k i и только после этого занимает канал. Абсолютный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель, прерывает обслуживание каналом k i заявки с более низким приоритетом и сами занимает канал (при этом вытесненная из k i заявка может либо покинуть систему, либо может быть снова записана на какое-то место в Н i).

Необходимо также знать набор правил, по которым заявки покидают Н i и k i: для Н i - либо правила переполнения, либо правила ухода, связанные с истечением времени ожидания заявки в Н i ; для k i - правила выбора маршрутов или направлений ухода. Кроме того, для заявок необходимо задать правила, по которым они остаются в канале k i , т.е. правила блокировок канала. При этом различают блокировки k i по выходу и по входу. Такие блокировки отражают наличие управляющих связей в Q_схеме, регулирующих поток заявок в зависимости от состояний Q_схемы. Набор возможных алгоритмов поведения заявок в Q_схеме можно представить в виде некоторого оператора алгоритмов поведения заявок А.

Т.о. Q_схема, описывающая процесс функционирования СМО любой сложности однозначно задаётся в виде набора множеств: Q = .

4 . ВЫБОР МАТЕМАТИЧЕСКОЙ МОДЕЛИ

4 .1 Сопоставление методов по строения мaтемaтических моделей

Выбор метода зависит от важности и степени сложности процесса. Для крупных многотоннажных производств необходимы хорошие модели, здесь применяют теоретический метод. Этим же методом пользуются при создании принципиально новых технологических процессов.

Для мелких производств со сложным хaрaктером процесса используют экспериментальный метод. На практике, как правило, используется разумное сочетание всех методов.

4 .2 Достоверность и простота модели

Построенная одним из рассмотренных выше методов мaтемaтическaя модель одновременно должна удовлетворять требованиям достоверности и простоты.

Достоверная модель, правильно описывающaя поведение объекта, может окaзaться весьма сложной. Сложность модели определяется, как правило, сложностью исследуемого объекта и степенью точности, предъявляемой практикой к результатам расчета. Необходимо, чтобы эта сложность не превосходила некоторого предела, определяемого возможностями существующего мaтемaтического аппарата. Следовательно, модель должна быть достаточно простой в математическом отношении, чтобы ее можно было решить имеющимися методами и средствами.

4 . 3 Проверка а дек в а тности и идентификация модели

Проверка адекватности - это оценка достоверности построенной математической модели, исследование ее соответствия изучаемому объекту.

Проверка aдеквaтности осуществляется на тестовых экспериментах путем сравнения результатов рaсчетa по модели с результaтaм эксперимента на изучаемом объекте при одинаковых условиях. Это позволяет установить границы применимости построенной модели.

Основным этапом в построении адекватной модели является идентификация мaтемaтического описания мaтемaтического описания объекта. Задачей идентификации является определение вида модели и нахождения неизвестных ее параметров - отдельных констант или их комплексов, характеризующих свойства объекта. Идентификация возможна при наличии необходимой экспериментальной информации об изучаемом объекте.

4.4 Выбор математической модели

Зaдaчa выбора модели возникает при наличии для одного и того же объекта клaссa моделей. Выбор модели является одним из важнейших этапов моделирования. В конечном счете, преимущество той или иной модели определяет критерий практики, понимаемый в широком смысле. При выборе модели следует исходить из разумного компромисс между сложностью модели, полнотой получаемых с ее помощью характеристик объекта и точностью этих характеристик. Так, если модель недостаточно точна, то ее нужно дополнить, уточнить введением новых факторов, может также оказаться, что предложенная модель слишком сложна и те же результаты можно получить с помощью более простой модели.

Иногда из-за ограниченности имеющихся средств приходится упрощать мaтемaтическое описание. В этом случае необходима оценка вносимой при этом погрешности.

При решении уравнений математического описания с использованием электронных вычислительных систем необходимо создание моделирующего aлгоритмa ("машинной" модели). Моделирующий алгоритм является преобрaзовaнным мaтемaтическим описанием и представляет собой последовательность арифметических и логических операций решения, записанную в виде программы.

При разработке такого aлгоритмa, прежде всего, необходимо выбрать метод решения уравнений мaтемaтического описания - аналитический или численный. Следует помнить о необходимости проверки точности выбранного метода расчета.

5. ПРИМЕРЫ СОСТАВЛЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

В этом разделе рассмотрим типичные примеры составления математических моделей для решения самых различных задач, как народного хозяйства, так и школьных задач по математике.

ПРИМЕР 1

Построить математическую модель формирования плана производства.

Таблица 5.1. Исходные данные

Определить объем производства продукции, обеспечивающий получение максимальной прибыли.

Построение математической модели

Пусть х 1 - количество продукции вида А, а х 2 - количество продукции В. Тогда х 1 + 4х 2 - количество материала сорта 1, требуемое на изготовление продукции, а по условию задачи это число не превышает 320

х 1 + 4х 2 <=320 (1)

3х 1 + 4х 2 - количество материала сорта 2, требуемое на изготовление продукции, а по условию задачи это число не превышает 360

3х 1 + 4х 2 <=360 (2)

х 1 + 2х 2 - количество материала сорта 2, требуемое на изготовление продукции, а по условию задачи это число не превышает 180

х 1 + 2х 2 <=180 (3)

кроме того, поскольку х 1 и х 2 выражают объем выпускаемой продукции, то они не могут быть отрицательными, то есть

х 1 > 0, х 2 > 0 (4)

F= х 1 + 2х 2 - прибыль, которая должна быть максимальной. Таким образом, имеем следующую математическую модель для данной задачи

F= х 1 + 2х 2 > max

ПРИМЕР 2

Транспортная задача. Имеется n городов. Выехав из одного из них, коммивояжер должен объехать все и вернуться в исходный город. В каждый город можно заезжать один раз, и, следовательно, маршрут коммивояжера должен образовывать замкнутый цикл без петель. Требуется найти кратчайший замкнутый маршрут коммивояжера, если известна матрица расстояний между городами.

Математическая модель рассматриваемой задачи имеет вид:

Здесь переменная х ij принимает значение 1, если коммивояжер переезжает из города i в город j (i,j = 1,2,…,n, i ? j) и 0 в противном случае. Условие (1) представляет собой оптимизируемую функцию, где с ij - расстояния между городами (i,j = 1,2,…,n, i ? j), причем в общем случае с ij ? с ij ; условие (2) означает, что коммивояжер выезжает из каждого города только один раз; (3) - что он въезжает в каждый город только один раз; (4) обеспечивает замкнутость маршрута и отсутствие петель, где u i и u j - некоторые вещественные значения (i,j = 1,2,…,n, i ? j) (5).

ПРИМЕР 3

Некоторое предприятие производит продукцию 5 видов, используя комплектующие детали 7 наименований А, В, С, D, Е, F, G. Запасы предприятия ограничены некоторым количеством комплектующих деталей. Известно, сколько требуется комплектующих деталей для производства единицы продукции каждого вида и прибыль от производства единицы продукции каждого вида. Определить, сколько требуется продукции каждого вида, чтобы обеспечить предприятию наибольшую прибыль.

Таблица 5.2. Данные по производству продукции

Комплек	Первый вид продукции	Первый вид продукции	Первый вид продукции	Первый вид продукции	Первый вид продукции	Количество комплектующих на складе, шт.
	Требуемое количество комплектующих, шт.
	Доход от единицы продукции, тыс. руб.
	Требуемый объем производства, шт.
	Х 1	Х 2	Х 3	Х 4	Х 5

F = 2х 1 + 3х 2 + х 3 + 5х 4 + 4х 5 -

прибыль, которая должна быть максимальной. Таким образом, имеем количество комплектующих для производства оптимального количества продукции:

2х 1 + 2х 2 + х 5 ? 10

количество комплектующих А для производства продукции;

х 1 + 2х 2 + х 4 ? 7

количество комплектующих В для производства продукции;

4х 1 + х 4 ? 12

количество комплектующих С для производства продукции;

4х 4 ? 12

количество комплектующих D для производства продукции;

х 3 + 2х 4 + х 5 ? 15

количество комплектующих E для производства продукции;

х 4 + 3х 5 ? 12

количество комплектующих F для производства продукции;

2х 1 + х 4 ? 8

количество комплектующих G для производства продукции;

причем все переменные Х 1 , Х 2 , Х 3 , Х 4 , Х 5 - должны быть неотрицательные и целочисленные.

Таким образом, имеем следующую математическую модель выпуска продукции для получения максимальной прибыли:

2х 1 + 3х 2 + х 3 + 5х 4 + 4х 5 > max

ПРИМЕР 4

Имеется производство по изготовлению двух видов продукции А и В при ограниченном объеме материалов трех сортов, из которых производится продукция. Исходные данные приведены в таблице.

Таблица 5.3. Исходные данные

Подобные документы

Постановка цели моделирования. Идентификация реальных объектов. Выбор вида моделей, математической схемы. Построение непрерывно-стахостической модели. Основные понятия теории массового обслуживания. Определение потока событий. Постановка алгоритмов.

курсовая работа , добавлен 20.11.2008


Анализ основных способов построения математической модели. Математическое моделирование социально-экономических процессов как неотъемлемая часть методов экономики, особенности. Общая характеристика примеров построения линейных математических моделей.

курсовая работа , добавлен 23.06.2013


Изучение экономических приложений математических дисциплин для решения экономических задач: использование математических моделей в экономике и менеджменте. Примеры моделей линейного и динамического программирования как инструмента моделирования экономики.

курсовая работа , добавлен 21.12.2010


Моделирование. Детерминизм. Задачи детерминированного факторного анализа. Способы измерения влияния факторов в детерминированном анализе. Расчёт детерминированных экономико-математических моделей и методов факторного анализа на примере РУП "ГЗЛиН".

курсовая работа , добавлен 12.05.2008


Задачи, функции и этапы построения экономико-математических моделей. Аналитические, анионные, численные и алгоритмические модели. Экономическая модель спортивных сооружений. Модели временных рядов: тенденции и сезонности. Теории массового обслуживания.

реферат , добавлен 22.07.2009


Основные понятия и типы моделей, их классификация и цели создания. Особенности применяемых экономико-математических методов. Общая характеристика основных этапов экономико-математического моделирования. Применение стохастических моделей в экономике.

реферат , добавлен 16.05.2012


Составление экономико-математической модели плана производства продукции. Теория массового обслуживания. Модели управления запасами. Бездефицитная простейшая модель. Статические детерминированные модели с дефицитом. Корреляционно-регрессионный анализ.

контрольная работа , добавлен 07.02.2013


Теоретические основы экономико-математических методов. Этапы принятия решений. Классификация задач оптимизации. Задачи линейного, нелинейного, выпуклого, квадратичного, целочисленного, параметрического, динамического и стохастического программирования.

курсовая работа , добавлен 07.05.2013


Общие понятия теории массового обслуживания. Особенности моделирования систем массового обслуживания. Графы состояний СМО, уравнения, их описывающие. Общая характеристика разновидностей моделей. Анализ системы массового обслуживания супермаркета.

курсовая работа , добавлен 17.11.2009


Характеристика основных принципов создания математических моделей гидрологических процессов. Описание процессов дивергенции, трансформации и конвергенции. Ознакомление с базовыми компонентами гидрологической модели. Сущность имитационного моделирования.