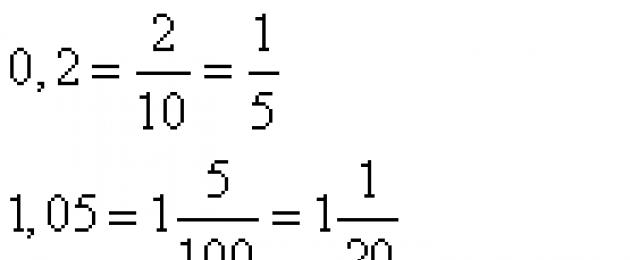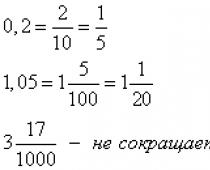無味乾燥な数学用語では、分数は 1 の一部として表される数値です。 分数は人間の生活の中で広く使用されています。料理のレシピで割合を示したり、競技会で小数点を与えたり、店舗での割引を計算するために分数を使用したりします。
分数の表現
1 つの分数を記述するには、10 進数形式と通常の分数形式の少なくとも 2 つの形式があります。 10 進数形式では、数値は 0.5 のように見えます。 0.25 または 1.375。 これらの値はいずれも普通の分数として表すことができます。
- 0,5 = 1/2;
- 0,25 = 1/4;
- 1,375 = 11/8.
そして、0.5 と 0.25 を普通の分数から小数に簡単に変換したり、逆に変換したりすると、数値 1.375 の場合、すべてが明らかではなくなります。 小数を素早く分数に変換するにはどうすればよいでしょうか? 簡単な方法が 3 つあります。
カンマを取り除く
最も単純なアルゴリズムでは、分子からカンマが消えるまで数値を 10 倍します。 この変換は次の 3 つの手順で実行されます。
ステップ1: まず、10 進数を分数「数値/1」として書きます。つまり、0.5/1 が得られます。 0.25/1 および 1.375/1。
ステップ2: この後、分子からカンマが消えるまで、新しい分数の分子と分母を掛けます。
- 0,5/1 = 5/10;
- 0,25/1 = 2,5/10 = 25/100;
- 1,375/1 = 13,75/10 = 137,5/100 = 1375/1000.
ステップ3: 得られた画分を消化可能な形に縮小します。
- 5/10 = 1 × 5 / 2 × 5 = 1/2;
- 25/100 = 1 × 25 / 4 × 25 = 1/4;
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8。
1.375 という数値は 10 を 3 回掛ける必要があり、あまり便利ではありませんが、0.000625 という数値を変換する必要がある場合はどうすればよいでしょうか? この状況では、次のような分数の変換方法を使用します。
カンマの削除がさらに簡単に
最初の方法では、小数点からカンマを「削除」するアルゴリズムを詳細に説明していますが、このプロセスは簡略化できます。 ここでも 3 つのステップに従います。
ステップ1: 小数点以下の桁数を数えます。 たとえば、数値 1.375 にはそのような桁が 3 つあり、0.000625 には 6 つあります。 この量を文字 n で表します。
ステップ2: ここで、分数を C/10 n の形式で表す必要があります。ここで、C は分数の有効桁 (ゼロがある場合は含まない)、n は小数点以下の桁数です。 例えば:
- 数値 1.375 C = 1375、n = 3 の場合、式 1375/10 3 = 1375/1000 による最終分数。
- 数値 0.000625 C = 625、n = 6 の場合、式 625/10 6 = 625/1000000 による最終分数。
本質的に、10n は 1 に n 個のゼロがあるため、わざわざ 10 をべき乗する必要はなく、1 に n 個のゼロを加えるだけです。 この後、ゼロが多く含まれる部分を減らすことをお勧めします。
ステップ3: ゼロを減らして最終結果を取得します。
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8;
- 625/1000000 = 1 × 625/1600 × 625 = 1/1600。
分数 11/8 は、分子が分母より大きいため、仮分数です。つまり、部分全体を分離できることを意味します。 この状況では、11/8 から 8/8 の全体を引いて、余り 3/8 が得られるため、分数は 1 と 3/8 のように見えます。
耳で変換
小数を正しく読める人にとって、それを変換する最も簡単な方法は、聞くことです。 0.025 を「ゼロ、ゼロ、二十五」ではなく「千分の 25」と読めば、問題なく小数を分数に変換できます。
0,025 = 25/1000 = 1/40
したがって、10 進数を正しく読み取ると、すぐに分数として書き留め、必要に応じて減らすことができます。
日常生活での分数の使用例
一見すると、普通の分数は日常生活や仕事ではほとんど使われず、学校の課題以外で小数を正分数に変換する必要がある状況を想像するのは困難です。 いくつかの例を見てみましょう。
仕事
あなたはキャンディーストアで働き、ハルヴァを量り売りしています。 製品を売りやすくするために、ハルバをキログラムの練炭に分割しますが、キログラム全体を購入する購入者はほとんどいません。 したがって、おやつを毎回分割する必要があります。 そして、次の買い手があなたに0.4kgのハルバを要求した場合、あなたは問題なく必要な分を彼に売るでしょう。
0,4 = 4/10 = 2/5
人生
たとえば、モデルを希望の色合いでペイントするには、12% の溶液を作成する必要があります。 これを行うには、塗料と溶剤を混合する必要がありますが、正しく行うにはどうすればよいでしょうか? 12% は 0.12 の小数です。 数値を公分数に変換すると、次のようになります。
0,12 = 12/100 = 3/25
分数を知ることで、材料を正しく混合し、希望の色を得ることができます。
結論
分数は日常生活でよく使用されるため、小数を分数に頻繁に変換する必要がある場合は、結果を短縮分数として即座に取得できるオンライン計算機を使用するとよいでしょう。
分数を使った数学の問題を解決しようとしているとき、学生は、これらの問題を解決したいという欲求だけでは十分ではないことに気づきます。 分数の計算の知識も必要です。 一部の問題では、すべての初期データが条件で分数形式で指定されます。 一部は分数であり、一部は整数である場合もあります。 これらの指定された値を使用して計算を実行するには、まず値を 1 つの形式にまとめてから、つまり整数を分数に変換してから計算を実行する必要があります。 一般に、整数を分数に変換する方法は非常に簡単です。 これを行うには、最後の分数の分子に指定された数値自体を書き込み、分母に 1 を書き込む必要があります。 つまり、数値 12 を分数に変換する必要がある場合、結果の分数は 12/1 になります。
このような変更は、分数を共通の分母にするのに役立ちます。 これは、分数の引き算や足し算を行うために必要です。 掛け算や割り算の際には公分母は必要ありません。 数値を分数に変換し、2 つの分数を加算する方法の例を見てみましょう。 数値 12 と小数 3/4 を加算する必要があるとします。 最初の項 (数値 12) は 12/1 の形式に縮小されます。 ただし、その分母は 1 に等しく、第 2 項の分母は 4 に等しくなります。これら 2 つの分数をさらに加算するには、それらを共通の分母にする必要があります。 数値の 1 つの分母が 1 であるため、これは通常は簡単です。 2 番目の数値の分母を取得し、最初の数値の分子と分母の両方にそれを掛ける必要があります。
乗算の結果は、12/1=48/4 となります。 48 を 4 で割ると 12 が得られます。これは、分数が正しい分母に減らされたことを意味します。 このようにして、分数を整数に変換する方法も理解できます。 これは、分子が分母より大きい仮分数にのみ適用されます。 この場合、分子を分母で割って余りがなければ整数になります。 余りがある場合、分数は分数のままですが、部分全体が強調表示されます。 次に、検討した例における共通の分母への還元について説明します。 最初の項の分母が 1 以外の他の数に等しい場合、最初の数の分子と分母に 2 番目の数の分母を乗算し、2 番目の数の分子と分母に 2 番目の数の分母を乗算する必要があります。初め。
両方の項は共通の分母に帰着され、加算する準備が整います。 この問題では、48/4 と 3/4 という 2 つの数値を加算する必要があることがわかります。 分母が同じ 2 つの分数を加算する場合は、それらの上部、つまり分子を合計するだけで済みます。 金額の分母は変わりません。 この例では、48/4+3/4=(48+3)/4=51/4 となります。 加算した結果がこうなります。 しかし、数学では、不適切な分数を正しい分数に減らすのが通例です。 分数を数値に変換する方法については上で説明しましたが、この例では、数値 51 は余りがなければ数値 4 で割り切れないため、分数 51/4 から整数は得られません。この分数の整数部分と小数部分。 整数部分は、51 未満の最初の数値を整数で割った数値になります。
つまり、4で割っても余りが出ないものです。 4 で完全に割り切れる、数字 51 の前の最初の数字は、数字 48 になります。48 を 4 で割ると、数字 12 が得られます。これは、必要な分数の整数部分が 12 になることを意味します。残るのは数値の小数部分を見つけるには。 小数部の分母は同じで、この場合は 4 です。 分数の分子を求めるには、元の分子から分母で割った数値を剰余なしで引く必要があります。 検討中の例では、数値 51 から数値 48 を引く必要があります。つまり、小数部の分子は 3 に等しいです。加算の結果は、12 の整数と 3/4 になります。 分数を引くときも同様です。 整数 12 から小数 3/4 を引く必要があるとします。 これを行うには、整数 12 が分数の 12/1 に変換され、2 番目の数である 48/4 との共通の分母になります。
同様に引き算する場合、両方の分数の分母は変更されず、分子で引き算が行われます。 つまり、2 番目の分子が最初の分数の分子から減算されます。 この例では、48/4-3/4=(48-3)/4=45/4 となります。 そして再び仮分数が得られたので、これを適切な分数に還元する必要があります。 部品全体を分離するには、剰余なしで 4 で割り切れる 45 までの最初の数値を決定します。 これは 44 になります。数値 44 を 4 で割ると、結果は 11 になります。これは、最後の分数の整数部分が 11 に等しいことを意味します。小数部分では、分母も変更されず、分子から元の仮分数から、余りを除いて分母で割った数値が減算されます。 つまり、45 から 44 を引く必要があります。これは、小数部の分子が 1、12-3/4=11 と 1/4 に等しいことを意味します。
1 つの整数と 1 つの分数が与えられ、その分母が 10 である場合、2 番目の数値を小数に変換して計算を実行する方が簡単です。 たとえば、整数 12 と小数 3/10 を加算する必要があります。 3/10 を小数として書くと、0.3 になります。 分数を公分母にして計算を実行し、仮分数から整数部分と小数部分を分離するよりも、0.3 を 12 に足して 2.3 を得る方がはるかに簡単です。 分数に関する最も単純な問題であっても、生徒 (または生徒) が整数を分数に変換する方法を知っていることを前提としています。 これらのルールは非常にシンプルなので覚えやすいです。 しかし、それらの助けを借りて、分数の計算を実行するのは非常に簡単です。
0.2 などの 10 進数。 1.05; 3.017など 聞かれたとおりに書かれます。 ゼロ ポイント 2、分数が得られます。 100 分の 1 ポイント 5 では分数が得られます。 17,000 分の 3 では、端数が得られます。 小数点の前の数字は分数の整数部分です。 小数点以下の数字は将来の分数の分子です。 小数点以下1桁の場合は分母が10、2桁の場合-100、3桁の場合-1000などとなります。 結果として得られる一部の分数を減らすことができます。 私たちの例では 
分数を小数に変換する
これは、前の変換の逆です。 小数部の特徴は何ですか? その分母は常に 10、100、1000、10000 などになります。 公分数の分母がこのようなものであれば問題ありません。 たとえば、または
たとえば分数が の場合。 この場合、分数の基本的な性質を利用して、分母を 10、100、または 1000 に変換する必要があります。この例では、分子と分母に 4 を掛けると、次のような分数が得られます。 10 進数 0.12 として記述されます。
一部の分数は、分母を変換するよりも割り算の方が簡単です。 例えば、
一部の分数は小数に変換できません。
例えば、
帯分数を仮分数に変換する
たとえば、帯分数は仮分数に簡単に変換できます。 これを行うには、分母 (下) を変更しないまま、部分全体に分母 (下) を掛け、分子 (上) を加えます。 あれは

帯分数を仮分数に変換するときは、分数の足し算が使えることを覚えておいてください。
仮分数を帯分数に変換(部分全体を強調表示)
仮分数は、全体を強調表示することで帯分数に変換できます。 例を見てみましょう。 「3」が「23」に入る整数倍を求めます。 または、電卓で 23 を 3 で割ると、小数点までの整数が求められます。 こちらは「7」です。 次に、将来の分数の分子を決定します。結果の「7」に分母「3」を掛け、その結果を分子「23」から引きます。 ![]() 分子の「23」から最大値の「3」を取り除いた余りが見つかるようなものです。 分母は変更しないままにします。 すべてが完了したので結果を書き留めます
分子の「23」から最大値の「3」を取り除いた余りが見つかるようなものです。 分母は変更しないままにします。 すべてが完了したので結果を書き留めます
この記事では、その方法を見ていきます 分数を小数に変換する、そしてその逆のプロセス、つまり小数を普通の分数に変換することも考えてみましょう。 ここでは、分数を変換するためのルールを概説し、典型的な例に対する詳細な解決策を示します。
ページナビゲーション。
分数を小数に変換する
対処する順序を示しましょう 分数を小数に変換する.
まず、分母が 10、100、1,000、... の分数を小数として表す方法を見ていきます。 これは、小数部の分数は本質的に、分母 10、100、... で通常の分数を記述するコンパクトな形式であるという事実によって説明されます。
その後、さらに進んで、通常の分数 (分母が 10、100 などの分数だけでなく) を小数として書く方法を示します。 常分数をこのように処理すると、有限小数と無限周期小数の両方が得られます。
それでは、すべてについて順番に話しましょう。
分母が 10、100、... の常用分数を小数に変換する
一部の適切な分数は、小数に変換する前に「事前準備」が必要です。 これは、分子の桁数が分母のゼロの数より少ない通常の分数に当てはまります。 たとえば、公用分数 2/100 は小数に変換するために最初に準備する必要がありますが、分数 9/10 は準備する必要がありません。
小数に変換するための適切な普通分数の「事前準備」は、分子の左側に多くのゼロを追加して、その合計桁数が分母のゼロの数と等しくなるようにすることで構成されます。 たとえば、ゼロを追加した後の分数は次のようになります。
適切な分数を準備したら、小数への変換を開始できます。
あげましょう 分母が 10、100、1,000 などの固有公分数を小数に変換する規則。 これは 3 つのステップで構成されます。
- 0を書き込みます。
- その後に小数点を置きます。
- 分子からの数値を書き留めます(ゼロを追加した場合は、追加したゼロも合わせて)。
例題を解くときにこのルールの適用を考えてみましょう。
例。
適切な分数 37/100 を小数に変換します。
解決。
分母にはゼロが 2 つある数値 100 が含まれています。 分子には数値 37 が含まれており、その表記は 2 桁であるため、この分数を小数に変換する準備をする必要はありません。
ここで、0 を書き、小数点を入力し、分子から 37 という数字を書くと、小数点 0.37 が得られます。
答え:
0,37 .
分子 10、100、... の適切な常分数を小数に変換するスキルを強化するために、別の例の解法を分析します。
例。
適切な分数 107/10,000,000 を小数として書きます。
解決。
分子の桁数は 3 で、分母のゼロの数は 7 であるため、この公分数は 10 進数に変換するために準備する必要があります。 分子の左側に 7-3=4 個のゼロを追加して、そこにある合計桁数が分母のゼロの数と等しくなるようにする必要があります。 我々が得る。
残っているのは、必要な小数部を作成することだけです。 これを行うには、最初に 0 を書き込み、次にカンマを入れ、最後に分子の数値をゼロと一緒に 0000107 と書き込みます。その結果、小数部 0.0000107 が得られます。
答え:
0,0000107 .
仮分数は、小数に変換するときに何の準備も必要ありません。 以下を遵守する必要があります 分母が 10、100、... の仮分数を小数に変換するためのルール:
- 分子からの数を書き留めます。
- 小数点を使用して、元の分数の分母にゼロがある数の右側の桁を区切ります。
例を解くときにこのルールを適用する方法を見てみましょう。
例。
仮分数 56,888,038,009/100,000 を小数に変換します。
解決。
まず、分子 56888038009 からの数値を書き留めます。次に、元の分数の分母にはゼロが 5 つあるため、右側の 5 桁を小数点で区切ります。 結果として、小数部 568880.38009 が得られます。
答え:
568 880,38009 .
帯分数を小数部分の分母が数値 10、100、または 1,000 などである小数に変換するには、帯分数を不適切な普通分数に変換し、その結果の分数を変換します。分数を小数に変換します。 ただし、次のようにすることもできます 分母が 10、100、または 1,000 などの帯分数を小数に変換する規則:
- 必要に応じて、分子の左側に必要な数のゼロを追加することで、元の帯分数の小数部の「予備準備」を実行します。
- 元の帯分数の整数部分を書き留めます。
- 小数点を入力します。
- 追加したゼロとともに分子からの数を書き留めます。
帯分数を小数として表すために必要な手順をすべて完了した例を見てみましょう。
例。
帯分数を 10 進数に変換します。
解決。
小数部分の分母にはゼロが 4 つありますが、分子には 2 桁の数字 17 が含まれているため、桁数が小数部の分母の数と等しくなるように、分子の左側にゼロを 2 つ追加する必要があります。分母にゼロが入っています。 これを行うと、分子は 0017 になります。
ここで、元の数値の整数部分、つまり数値 23 を書き留め、小数点を置き、その後、分子からの数値と追加のゼロ (つまり 0017) を書き込みます。すると、目的の小数が得られます。端数 23.0017。
ソリューション全体を簡単に書き留めてみましょう。 ![]() .
.
もちろん、帯分数を仮分数で表してから小数に変換することも可能です。 このアプローチを使用すると、ソリューションは次のようになります。
答え:
23,0017 .
分数を有限および無限の周期小数に変換する
分母が 10、100、... の普通分数だけでなく、他の分母の普通分数も小数に変換できます。 次に、これがどのように行われるかを見ていきます。
場合によっては、元の普通分数は分母 10、100、1,000 などのいずれかに簡単に減算されます (普通分数を新しい分母にするを参照)。その後、結果の分数を表すのは難しくありません。小数として。 たとえば、分数 2/5 は分母 10 の分数に分解できることは明らかです。そのためには、分子と分母に 2 を掛ける必要があります。これにより、分数 4/10 が得られます。前の段落で説明したルールは、小数 0, 4 に簡単に変換できます。
他の場合には、普通の分数を小数に変換する別の方法を使用する必要があります。これについては次に検討します。
普通の分数を小数分数に変換するには、分数の分子を分母で割ります。分子はまず、小数点以下に任意の数のゼロを含む等しい小数に置き換えられます (これについては、「等しいと」のセクションで説明しました)。小数が等しくない場合)。 この場合の割り算は、自然数の列による割り算と同じように行われ、被除数全体の割り算が終了した時点で商に小数点が置かれます。 これらすべては、以下に示す例の解決策から明らかになるでしょう。
例。
分数 621/4 を 10 進数に変換します。
解決。
分子 621 の数値を小数点とその後にいくつかのゼロを追加して、小数として表してみましょう。 まず、2 桁の 0 を追加します。後で、必要に応じて、いつでもゼロを追加できます。 したがって、621.00 になります。
次に、列を使用して数値 621,000 を 4 で割ってみましょう。 最初の 3 つのステップは自然数を列で割ることと何ら変わりません。その後、次の図が得られます。 
このようにして配当の小数点に到達し、剰余はゼロとは異なります。 この場合、商に小数点を入れて、カンマに注意せずに列内の分割を続けます。 
これで割り算が完了し、その結果、元の普通分数に相当する小数部 155.25 が得られます。
答え:
155,25 .
資料を統合するために、別の例の解決策を検討してください。
例。
小数部 21/800 を 10 進数に変換します。
解決。
この公分数を小数に変換するには、小数の列 21,000... を 800 で割ります。 最初のステップの後、商に小数点を入れて、割り算を続ける必要があります。 
最後に、余り 0 が得られ、公分数 21/400 から小数への変換が完了し、小数 0.02625 が得られました。
答え:
0,02625 .
普通の分数の分子を分母で割ったときに、それでも余りが 0 にならないことがあります。 このような場合、分割は無限に継続される可能性があります。 しかし、あるステップからは、余りが周期的に繰り返され、商の数字も繰り返されます。 これは、元の分数が無限の周期小数に変換されることを意味します。 これを例で示してみましょう。
例。
分数 19/44 を小数として書きます。
解決。
普通の分数を小数に変換するには、列による除算を実行します。 
割り算では剰余 8 と 36 が繰り返され始め、商では数字 1 と 8 が繰り返されることはすでに明らかです。 したがって、元の公分数 19/44 は周期小数分数 0.43181818...=0.43(18) に変換されます。
答え:
0,43(18) .
この点の結論として、どの常分数が有限小数に変換できるのか、どの常分数が周期分数にしか変換できないのかを明らかにします。
既約常分数が目の前にあるとします (分数が約分できる場合は、まず分数を約分します)。そして、それがどの小数に変換できるか (有限または周期) を調べる必要があります。
普通の分数を分母 10、100、1,000、... のいずれかに減らすことができれば、得られた分数は、前の段落で説明したルールに従って、最終的な小数に簡単に変換できることは明らかです。 ただし、分母には 10、100、1,000 などがあります。 すべての普通の分数が与えられるわけではありません。 分母が数値 10、100、... の少なくとも 1 つである分数のみが、そのような分母に約分できます。また、10、100、... の約数となる数値は何ですか? この質問には 10、100、... という数字が答えになります。10 = 2 5、100 = 2 2 5 5、1,000 = 2 2 2 5 5 5、... となります。 したがって、約数は 10、100、1,000 などになります。 素因数への分解に数値 2 と (または) 5 のみが含まれる数値のみが存在します。
これで、通常の分数を小数に変換することについて一般的な結論を下すことができます。
- 分母を素因数に分解する際に数値 2 と (または) 5 のみが存在する場合、この分数は最終的な小数に変換できます。
- 2 と 5 に加えて、分母の展開に他の素数がある場合、この分数は無限小数の周期分数に変換されます。
例。
普通の分数を小数に変換せずに、分数 47/20、7/12、21/56、31/17 のどれが最終小数に変換でき、どれが周期分数にのみ変換できるかを教えてください。
解決。
分数 47/20 の分母は、20=2・2・5 のように素因数分解されます。 この展開では 2 と 5 しかないため、この分数は分母 10、100、1,000、... (この例では分母 100) のいずれかに減らすことができ、最終的な 10 進数に変換できます。分数。
分数 7/12 の分母を素因数に分解すると、12=2・2・3 の形式になります。 2 や 5 とは異なり、素因数 3 が含まれるため、この分数は有限小数として表すことはできませんが、周期小数に変換できます。
分数 21/56 – 収縮性、収縮後は 3/8 の形になります。 分母を素因数に因数分解すると、2 に等しい因数が 3 つ含まれるため、公分数 3/8、つまり等しい分数 21/56 を最終的な小数に変換できます。
最後に、分数 31/17 の分母の展開は 17 そのものであるため、この分数は有限小数には変換できませんが、無限周期分数には変換できます。
答え:
47/20 と 21/56 は有限小数に変換できますが、7/12 と 31/17 は周期分数にのみ変換できます。
普通の分数は無限の非周期小数に変換されません
前の段落の情報から、「分数の分子を分母で割ると、無限の非周期分数が得られるでしょうか?」という疑問が生じます。
答え: いいえ。 公分数を変換すると、結果は有限小数または無限周期小数のいずれかになります。 その理由を説明しましょう。
剰余による割り算の定理から、剰余は常に除数より小さいことが明らかです。つまり、ある整数を整数 q で割った場合、剰余は 0、1、2 のいずれか 1 つのみになります。 , ..., q−1. したがって、列が普通分数の分子の整数部分を分母 q で除算し終えた後、q ステップ以内に次の 2 つの状況のいずれかが発生します。
- または、剰余 0 が得られ、これで除算が終了し、最後の小数が得られます。
- または、以前にすでに出現した剰余を取得し、その後、前の例と同様に剰余が繰り返されます (等しい数を q で割ると等しい剰余が得られ、これはすでに述べた割り算定理から得られるため)。無限の周期小数になります。
他に選択肢がないため、普通分数を小数に変換する場合、無限の非周期小数を求めることはできません。
この段落で与えられた推論から、小数の周期の長さは常に、対応する普通分数の分母の値よりも小さいということになります。
小数を分数に変換する
ここで、小数を普通の分数に変換する方法を考えてみましょう。 最終的な小数を普通の分数に変換することから始めましょう。 この後、無限周期小数を反転する方法を考えます。 結論として、無限の非周期小数を普通の分数に変換することは不可能であるということについて話しましょう。
末尾の小数を分数に変換する
最終小数として書かれた分数を取得するのは非常に簡単です。 最終小数部を公分数に変換するための規則次の 3 つのステップで構成されます。
- まず、与えられた小数を分子に書き込みます。小数点と左側のゼロがあればすべて破棄します。
- 次に、分母に 1 を書き込み、元の小数部の小数点以下の桁数と同じ数のゼロを追加します。
- 第三に、必要に応じて、結果の端数を減らします。
例の解決策を見てみましょう。
例。
小数の 3.025 を分数に変換します。
解決。
元の小数から小数点を削除すると、3,025 という数値が得られます。 左側には破棄できるゼロはありません。 したがって、必要な分数の分子に 3,025 を書き込みます。
元の小数では小数点以下が 3 桁あるため、分母に数値 1 を書き込み、その右側に 3 つのゼロを追加します。
したがって、公分数 3,025/1,000 が得られました。 この端数は 25 で減らすことができ、次のようになります。  .
.
答え:
 .
.
例。
小数部 0.0017 を分数に変換します。
解決。
小数点がないと、元の小数は 00017 のようになり、左側のゼロを破棄すると、数値 17 が得られます。これは、目的の普通分数の分子です。
元の小数は小数点以下 4 桁なので、分母にゼロが 4 つある 1 と書きます。
その結果、普通端数は 17/10,000 になります。 この分数は既約であり、小数分数から通常の分数への変換が完了します。
答え:
 .
.
元の最終小数部の整数部がゼロ以外の場合、公用分数をバイパスして直ちに帯分数に変換できます。 あげましょう 最終的な小数を帯分数に変換するための規則:
- 小数点の前の数値は、希望する帯分数の整数部分として書き込む必要があります。
- 小数部分の分子には、左側のゼロをすべて捨てた後、元の小数の小数部分から取得した数値を記述する必要があります。
- 小数部の分母には数値 1 を書き留める必要があり、その数値の右側に、元の小数部の小数点以下の桁数と同じ数のゼロが追加されます。
- 必要に応じて、得られた混合数の小数部分を減算します。
小数を帯分数に変換する例を見てみましょう。
例。
小数部 152.06005 を帯分数として表現します
497 を 4 で割る必要がある場合、割るときに 497 が 4 で均等に割り切れないことがわかります。 部門の残りは残ります。 このような場合は完了したと言われます 余りによる除算、解決策は次のように書かれています。
497: 4 = 124 (余り 1)。
等式の左側の除算コンポーネントは、剰余なしの除算と同じように呼び出されます。 497 - 配当, 4 - ディバイダー。 剰余で割ったときの除算結果は と呼ばれます。 不完全なプライベート。 私たちの場合、これは数値 124 です。そして最後に、通常の除算ではない最後の成分は次のとおりです。 残り。 余りがない場合は、ある数を別の数で割ったと言われます 跡形もなく、または完全に。 このような除算では、剰余はゼロになると考えられています。 この場合、余りは 1 です。
剰余は常に除数より小さくなります。
割り算は掛け算で確認できます。 たとえば、64: 32 = 2 という等式がある場合、チェックは次のように行うことができます: 64 = 32 * 2。
剰余ありの除算を行う場合、等式を使用すると便利なことがよくあります。
a = b * n + r、
ここで、a は被除数、b は除数、n は部分商、r は剰余です。
自然数の商は分数として書くことができます。
分数の分子は被除数、分母は約数です。
分数の分子は被除数、分母は約数なので、 分数の線は割り算を意味すると信じている。 「:」記号を使用せずに、割り算を分数として記述すると便利な場合があります。
自然数 m と n の除算の商は、分数 \(\frac(m)(n) \) として書くことができます。ここで、分子 m は被除数、分母 n は約数です。
\(m:n = \frac(m)(n)\)
次のルールが当てはまります。
分数 \(\frac(m)(n)\) を取得するには、単位を n 個の等しい部分 (シェア) に分割し、その部分を m 個取る必要があります。
分数 \(\frac(m)(n)\) を取得するには、数値 m を数値 n で割る必要があります。
全体の一部を求めるには、全体に対応する数値を分母で割り、その結果にこの部分を表す分数の分子を掛ける必要があります。
部分から全体を見つけるには、この部分に対応する数値を分子で割り、その結果にこの部分を表す分数の分母を掛ける必要があります。
分数の分子と分母の両方に同じ数値 (ゼロを除く) を掛けても、分数の値は変わりません。
\(\large \frac(a)(b) = \frac(a \cdot n)(b \cdot n) \)
分数の分子と分母の両方が同じ数 (ゼロを除く) で除算される場合、分数の値は変わりません。
\(\large \frac(a)(b) = \frac(a: m)(b: m) \)
このプロパティはと呼ばれます 分数の主な性質.
最後の 2 つの変換は次のように呼ばれます。 分数を減らす.
分数を同じ分母を持つ分数として表す必要がある場合、このアクションは呼び出されます。 分数を共通の分母にする.
適正分数と仮分数。 帯分数
全体を等しい部分に分割し、その部分をいくつか取ると分数が得られることはすでにご存知でしょう。 たとえば、分数 \(\frac(3)(4)\) は 1 の 4 分の 3 を意味します。 前の段落の問題の多くでは、全体の一部を表すために分数が使用されていました。 常識では、部分は常に全体より小さくなければなりませんが、\(\frac(5)(5)\) や \(\frac(8)(5)\) のような分数の場合はどうでしょうか。 これがもはやユニットの一部ではないことは明らかです。 おそらくこれが、分子が分母以上の分数と呼ばれる理由です。 仮分数。 残りの分数、つまり分子が分母より小さい分数は、と呼ばれます。 正しい分数.
ご存知のとおり、公分数は、適正分数と不適正分数の両方で、分子を分母で割った結果と考えることができます。 したがって、数学では、通常の言語とは異なり、「仮分数」という用語は、何か間違ったことをしたという意味ではなく、この分数の分子が分母以上であることだけを意味します。
数値が整数部と小数部で構成されている場合、そのような 分数は混合と呼ばれます.
例えば:
\(5:3 = 1\frac(2)(3) \) : 1 は整数部分、\(\frac(2)(3) \) は小数部分です。
分数 \(\frac(a)(b)\) の分子が自然数 n で割り切れる場合、この分数を n で割るためには、その分子を次の数で割る必要があります。
\(\large \frac(a)(b) : n = \frac(a:n)(b) \)
分数 \(\frac(a)(b)\) の分子が自然数 n で割り切れない場合、この分数を n で割るには、分母に次の数を掛ける必要があります。
\(\large \frac(a)(b) : n = \frac(a)(bn) \)
2 番目のルールは、分子が n で割り切れる場合にも当てはまります。 したがって、分数の分子がnで割り切れるかどうかが一見して判断しにくい場合に利用できます。
分数を使用したアクション。 分数の加算。
自然数と同様に、小数を使った算術演算を実行できます。 まずは分数の足し算を見てみましょう。 分母が似ている分数の足し算は簡単です。 たとえば、\(\frac(2)(7)\) と \(\frac(3)(7)\) の合計を求めてみましょう。 \(\frac(2)(7) + \frac(2)(7) = \frac(5)(7) \) というのがわかりやすいですね。
同じ分母を持つ分数を加算するには、分母を同じにして分子を加算する必要があります。
文字を使用すると、分母が似ている分数を加算するルールは次のように記述できます。
\(\large \frac(a)(c) + \frac(b)(c) = \frac(a+b)(c) \)
分母の異なる分数を加算する必要がある場合は、まずそれらを共通の分母に減らす必要があります。 例えば:
\(\large \frac(2)(3)+\frac(4)(5) = \frac(2\cdot 5)(3\cdot 5)+\frac(4\cdot 3)(5\cdot 3 ) = \frac(10)(15)+\frac(12)(15) = \frac(10+12)(15) = \frac(22)(15) \)
分数については、自然数と同様に、加算の可換性および結合性が有効です。
帯分数の加算
\(2\frac(2)(3)\) などの表記法が呼び出されます。 混合分数。 この場合、数字の 2 が呼び出されます。 全体帯分数、数値 \(\frac(2)(3)\) はその値です 小数部。 エントリ \(2\frac(2)(3)\) は、「2 と 3 分の 2」と読み取られます。
数値 8 を数値 3 で割ると、\(\frac(8)(3)\) と \(2\frac(2)(3)\) の 2 つの答えが得られます。 これらは同じ分数を表します。つまり \(\frac(8)(3) = 2 \frac(2)(3)\)
したがって、仮分数 \(\frac(8)(3)\) は帯分数 \(2\frac(2)(3)\) として表されます。 このような場合、彼らは仮分数からと言います。 部分全体を強調表示した.
分数の引き算(小数)
自然数と同様、分数の減算は加算の作用に基づいて決定されます。ある数値から別の数値を引くということは、2 番目の数値に加算すると 1 番目の数値が得られる数値を見つけることを意味します。 例えば:
\(\frac(8)(9)-\frac(1)(9) = \frac(7)(9) \) 以来 \(\frac(7)(9)+\frac(1)(9 ) = \frac(8)(9)\)
分母が似ている分数を減算するルールは、そのような分数を加算するルールと似ています。
同じ分母を持つ分数間の差を求めるには、最初の分数の分子から 2 番目の分数の分子を引き、分母は同じにしておく必要があります。
文字を使用すると、このルールは次のように記述されます。
\(\large \frac(a)(c)-\frac(b)(c) = \frac(a-b)(c) \)
分数の掛け算
分数と分数を掛けるには、分子と分母を掛けて、最初の積を分子として、2 番目の積を分母として書く必要があります。
文字を使用すると、分数の掛け算のルールは次のように記述できます。
\(\large \frac(a)(b) \cdot \frac(c)(d) = \frac(a \cdot c)(b \cdot d) \)
定式化されたルールを使用すると、分数と自然数、帯分数を掛けたり、帯分数を掛けたりすることができます。 これを行うには、分母が 1 の分数、帯分数、つまり仮分数として自然数を記述する必要があります。
乗算の結果は、分数を削減し、仮分数の部分全体を分離することによって (可能であれば) 単純化する必要があります。
分数については、自然数と同様に、乗算の可換性および結合性、ならびに加算に対する乗算の分配性が有効です。
分数の割り算
分数 \(\frac(2)(3)\) を「反転」して、分子と分母を入れ替えてみましょう。 分数 \(\frac(3)(2)\) が得られます。 この分数はと呼ばれます 逆行する分数 \(\frac(2)(3)\)。
ここで分数 \(\frac(3)(2)\) を「反転」すると、元の分数 \(\frac(2)(3)\) が得られます。 したがって、 \(\frac(2)(3)\) や \(\frac(3)(2)\) などの分数は呼び出されます。 相互に反転.
たとえば、分数 \(\frac(6)(5) \) と \(\frac(5)(6) \)、\(\frac(7)(18) \) と \(\frac (18) )(7)\)。
文字を使用すると、逆分数は次のように書くことができます: \(\frac(a)(b) \) および \(\frac(b)(a) \)
は明らかです 逆数の積は 1 に等しい。 例: \(\frac(2)(3) \cdot \frac(3)(2) =1 \)
逆分数を使用すると、分数の割り算を掛け算に変換できます。
分数を分数で割る規則は次のとおりです。
ある分数を別の分数で割るには、被除数に除数の逆数を掛ける必要があります。
文字を使用すると、分数の割り算ルールは次のように記述できます。
\(\large \frac(a)(b) : \frac(c)(d) = \frac(a)(b) \cdot \frac(d)(c) \)
被除数または除数が自然数または帯分数の場合、分数の割り算ルールを使用するには、まず仮分数として表す必要があります。